Ko te kaupapa nei, he tūhura i ngā ōwehenga pākoki e rua nei, te aho (sin) me te whenu (cosine). Ka tirohia ngā ōwehenga o ngā tapa o tētahi tapatoru hāngai, me te whakamahinga o aua ōwehenga hei tātai i tētahi tapa, hei tātai rānei i tētahi o ngā koki.
Kia mōhio te ākonga ki:
- ngā tikanga mō te whakaingoa i ngā tapa o tētahi tapatoru hāngai, arā, ko te tāroa, te tapa pātata me te tapa hāngai.
- te tuhi hoahoa āwhata o te tapatoru hāngai, ka ine ai i te roa o ngā tapa. Mā konei e whakaputa ai i ngā ōwehenga pākoki mō te aho (sin) me te whenu (cosine)
- te whakamahi i ngā ōwehenga pākoki o te aho (sin) me te whenu (cosine) hei tātai i te roa o tētahi tapa o te tapatoru hāngai, i tētahi koki rānei.
- te whakamahi i ngā pūtohu ‘sin’, ‘cos’, ‘sin-1’, cos-1 o te tātaitai.
Whārangi Mahi 4
Whārangi Mahi 3
Whārangi Mahi 2
Whārangi Mahi 1
he tātaitai
Whārangi Mahi 5
he ruri
he ine-koki
Whārangi Mahi 6
|
aho
|
sin
|
|
inverse sin (sin-1)
|
|
|
ōwehenga pākoki
|
trigonometric ratio
|
|
ōwehenga tapa aho
|
sine ratio
|
|
ōwehenga whenu
|
cosine ratio
|
|
trigonometry
|
|
|
tapa hāngai
|
opposite side
|
|
tapa pātata
|
adjacent side
|
|
tāroa
|
hypotenuse
|
|
whenu
|
cosine
|
|
inverse cosine (cos-1)
|
- Ko te mahi tuatahi, he whakamārama i te tikanga mō te whakaingoa i ngā tapa o tētahi tapatoru hāngai.
Te mahi a te pouako He tauira kōrero mā te pouako Tuhia tētahi tapatoru hāngai ki te papa tuhituhi, ka whakawhitiwhiti kōrero ai mō te whakaingoa i ngā tapa. Anei tētahi tapatoru hāngai.

He aha e kīia ai he tapatoru hāngai tēnei? Nā te mea he koki hāngai tōna.
Me pēhea te waitohu i te koki hāngai? Tuhia he tapawhā rite paku ki taua koki.

Māku e waitohu tētahi atu o ngā koki o te tapatoru. Ka whakamahia tētahi pū kiriki, ko ‘theta’ te ingoa.
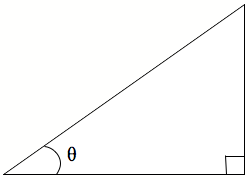
Ināianei ka hoatu ingoa ki ngā tapa o te tapatoru hāngai. Ko tētahi ko te tapa pātata. Arā, he pātata ki te koki e waitohua ana ki te pū ‘theta’.
Ko tētahi tapa ka kīia ko te tapa hāngai, ina e noho hāngai ana taua tapa ki te koki ‘theta’.
Ko te tapa tuatoru ka kīia ko te tāroa nā te mea koia te tapa roa rawa atu o te tapatoru.
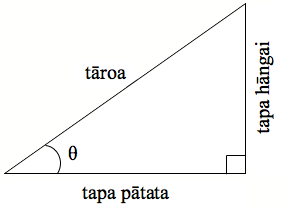
Whakaaturia ētahi atu tapatoru hāngai, ka tono ai i ngā ākonga ki te whakaingoa i ngā tapa. Kei Whārangi Mahi 1 (PDF, 92KB)ētahi hei whakaoti mā ngā ākonga.
- Ko te mahi tuarua, he tūhura i te ōwehenga mō te whenu (cos) mō te 30°.
Te mahi a te pouako He tauira kōrero mā te pouako Tonoa ngā ākonga ki te tuhi i tētahi tapatoru hāngai ki ā rātou pukapuka. Kia 30° te rahi o tētahi o ngā koki. Kei a rātou te rahi o te tapatoru (e tika ana kia rerekē te rahi o te tapatoru o tēnā o tēnā o ngā ākonga). Whakamahia te ine-koki me te ruri hei tuhi i tētahi tapatoru hāngai ki ā koutou pukapuka. Kei a koe te whakatau i te rahi o te tapatoru, engari kia 90° te rahi o tētahi o ngā koki, kia 30° te rahi o tētahi.
Waitohua te koki hāngai me te koki 30°.
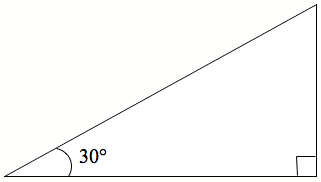
Inea te tāroa me te tapa pātata o tō tapatoru hāngai, ka tuhi atu ai ki te pikitia.
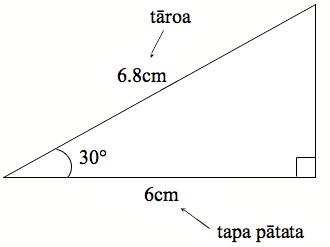
Tuhia ngā inenga o ngā tapa ki tētahi tūtohi, ka whakawhitiwhiti kōrero ai mō te ōwehenga whenu Māku e tuhi ngā inenga o ngā tapa ki tētahi tūtohi:
ākonga tāroa (cm) tapa
pātata (cm)Aroha 6.8 6 Rongopai 4 3.5 Horomona 4.5 4 Manahi 7 6 … Whakamahia he tātaitai hei whakawehe i te inenga mō te tapa pātata ki te inenga mō te tāroa. Tuhia ki te tūtohi.:
ākonga tāroa (cm) tapa pātata (cm) ōwehenga whenu
(2mi)Aroha 6.8 6 0.88 Rongopai 4 3.5 0.88 Horomona 4.5 4 0.89 Manahi 7 6 0.86 … Ka whakaingoatia tēnei pou o te tūtohi, ko te ōwehenga whenu. Koirā te wehenga o te tapa pātata ki te tāroa. He aha tētahi mea e kitea mai ana? Ahakoa he rerekē te rahi o ngā tapatoru, he āhua ōrite te ōwehenga whenu.
Ko te 0.87 te ōwehenga whenu mō te 30°. Arā, mēnā 1 cm te tāroa, 0.87 cm te roa o te tapa pātata:
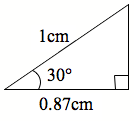
Ko te whakapotonga o te ‘ōwehenga whenu’ ko te ‘cos’, he whakapotonga o te kupu Ingarihi ‘cosine’. Kia pēnei te tuhi: cos(30°) = 0.87
Tuhia ngā tapatoru hāngai nei ki te papa tuhituhi, ka whakawhitiwhiti kōrero ai mō te tātai ai i te roa o ngā tapa. Anei ētahi tapatoru hāngai e rua. He ōrite te āhua o ēnei tapatoru hāngai nā te mea e 30° te rahi o tētahi koki o ngā tapatoru e rua. He whakarahinga tētahi i tētahi.
.jpg)
He pēhea nei te rahinga ake o tētahi i tētahi? He whakarea ki te 4. E 4 te whakareatanga ake o tētahi i tētahi.
Nō reira me pēhea te tātai i te roa o te tapa ‘k’? Whakareatia te 0.87 ki te 4.
Ka tika. Me pēnei te tuhi i te tātaitanga:
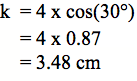
Whakamāramatia te whakamahinga o te pūtohu ‘cos’ i te tātaitai. Titiro ki ā koutou tātaitai. Kei konā he pūtohu kua tapaina ki te ‘cos’. Whakaurua te 30 mō te 30°, ka pēhi ai i te pūtohu ‘cos’. He aha te whakaputanga? Ko te 0.8660254.
Ki te whakaawhiwhia kia rua ngā mati a-ira, ko te 0.87. Koirā te ōwehenga whenu mō te 30°, arā, cos(30°) = 0.8660254
Whakamahia te tātaitai hei whiriwhiri i te tapa pātata o ētahi tapatoru hāngai. Kei Whārangi Mahi 2 (PDF, 96KB)
- Ko te mahi tuatoru, he tūhura i te ōwehenga aho (sin), mō te 30°. (He ōrite ki te mahi i runga nei mō te ōwehenga whenu (cosine).
Te mahi a te pouako He tauira kōrero mā te pouako Tonoa ngā ākonga ki te tuhi i tētahi tapatoru hāngai ki ā rātou pukapuka. Kia 30° te rahi o tētahi o ngā koki. Kei a rātou te rahi o te tapatoru (e tika ana kia rerekē te rahi o te tapatoru o tēnā o tēnā o ngā ākonga). Whakamahia te ine-koki me te ruri hei tuhi i tētahi tapatoru hāngai ki ā koutou pukapuka. Kei a koe te whakatau i te rahi o te tapatoru, engari kia 90° te rahi o tētahi o ngā koki, kia 30° te rahi o tētahi.
Waitohua te koki hāngai me te koki 30°.
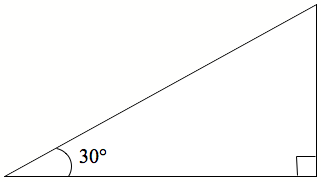
Inea te tāroa me te tapa hāngai o tō tapatoru, ka tuhi atu ai ki te pikitia.
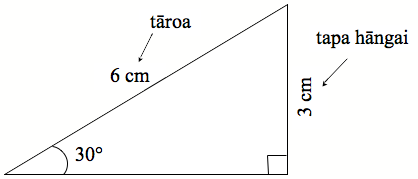
Tuhia ngā inenga o ngā tapa ki tētahi tūtohi, ka whakawhitiwhiti kōrero ai mō te ōwehenga whenu Māku e tuhi ngā inenga o ngā tapa ki tētahi tūtohi:
ākonga tāroa (cm) tapa pātata
(cm)Aroha 6.8 3.4 Rongopai 4 2 Horomona 4.5 2.3 Manahi 7 3.5 … Whakamahia he tātaitai hei whakawehe i te inenga mō te tapa hāngai ki te inenga mō te tāroa. Tuhia ki te tūtohi:
ākonga tāroa (cm) tapa
pātata
(cm)ōwehenga
aho (2mi)Aroha 6.8 6 0.5 Rongopai 4 3.5 0.5 Horomona 4.5 4 0.5 Manahi 7 6 0.5 … Ka whakaingoatia tēnei pou o te tūtohi, ko te ōwehenga aho. Koirā te wehenga o te tapa hāngai ki te tāroa. He aha tētahi mea e kitea mai ana? Ahakoa he rerekē te rahi o ngā tapatoru, he ōrite te ōwehenga aho.
Ko te 0.5 te ōwehenga aho mō te 30°. Arā, mēnā 1 cm te tāroa, 0.5 cm te roa o te tapa hāngai:
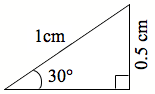
Ko te whakapotonga o te ‘ōwehenga ahoi’ ko te ‘sin’, he whakapotonga o te kupu Ingarihi ‘sine’. Kia pēnei te tuhi: sin(30°) = 0.5
Tuhia ngā tapatoru hāngai nei ki te papa tuhituhi, ka whakawhitiwhiti kōrero ai mō te tātai ai i te roa o ngā tapa. Anei ētahi tapatoru hāngai e rua. He ōrite te āhua o ēnei tapatoru hāngai nā te mea e 30° te rahi o tētahi koki o ngā tapatoru e rua. He whakarahinga tētahi i tētahi.
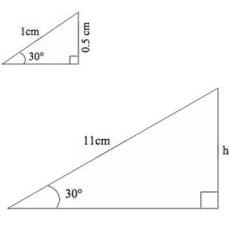
He pēhea nei te rahinga ake o tētahi i tētahi? He whakarea ki te 11. Tekau mā tahi te whakareatanga ake o tētahi i tētahi. Nō reira me pēhea te tātai i te roa o te tapa ‘h’? Whakareatia te 0.5 ki te 11. Ka tika. Me pēnei te tuhi i te tātaitanga:
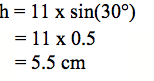
Whakamāramatia te whakamahinga o te pūtohu ‘sin’ i te tātaitai. Titiro ki ā koutou tātaitai. Kei konā he pūtohu kua tapaina ki te ‘sin’. Whakaurua te 30 mō te 30°, ka pēhi ai i te pūtohu ‘sin’. He aha te whakaputanga? Ko te 0.5.
Koirā te ōwehenga aho mō te 30°, arā, sin(30°) = 0.5
Whakamahia te tātaitai hei whiriwhiri i te tapa hāngai o ētahi tapatoru hāngai. Kei Whārangi Mahi 3 (PDF, 103KB)
- Ko te mahi tuawhā, he tūhura i te ōwehenga aho (sin), me te whenu (cosine) mō ētahi atu rahinga koki (He ōrite ki te mahi i runga nei mō te ōwehenga whenu (cosine).
Kia pērā anō te arataki i ngā ākonga ki te tūhura i te ōwehenga aho (sin) me te ōwehenga whenu (cosine) mō ētahi atu koki.
Ka mutu, kia pēnei pea te whakaatu i ngā ōwehenga nei:
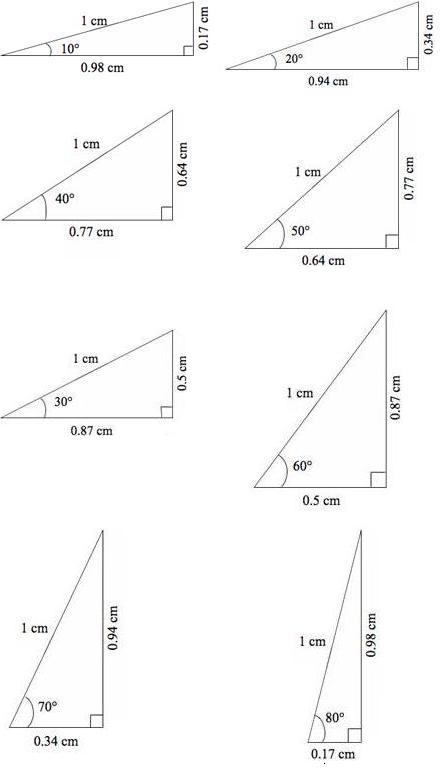
Whakaaturia hoki ngā ōwehenga nei ki tētahi tūtohi, ka whakawhitiwhiti kōrero ai mō te tauira e kitea mai ana:
koki ōwehenga whenu (cos) ōwehenga aho (sin) 10° 0.98 0.17 20° 0.94 0.34 30° 0.87 0.5 40° 0.77 0.64 50° 0.64 0.77 60° 0.5 0.87 70° 0.34 0.94 80° 0.17 0.98 Whakawhitiwhiti kōrero mō te take kāore he uara mō te ōwehenga whenu me te ōwehenga aho mō te 90°, mō te 0° rānei. Nā te mea kāore e taea tētahi tapatoru hāngai te tuhi e rua ōna koki hāngai, kotahi rānei te koki hāngai me tētahi koki 0° te rahi.
Hoatu he rapanga pērā i ērā i Whārangi Mahi 4 (PDF, 98KB)
- Whakawhitiwhiti kōrero mō te tātai i te tāroa o tētahi tapatoru hāngai mēnā e mōhiotia ana te tapa pātata, te tapa hāngai rānei.
Te mahi a te pouako He tauira kōrero mā te pouako Tuhia tētahi tapatoru hāngai ki te papa tuhituhi e whakaatu ana i tētahi koki me te roa o tētahi o ngā tapa poto:
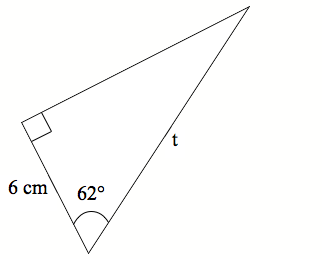
Titiro ki te tapatoru hāngai nei. E whakaaturia ana tētahi o ngā koki. He aha te ingoa o te tapa e 6 cm te roa? Koia ko te tapa pātata, nā te mea e noho pātata ana ki te koki e whakaaturia ana.
Me pēhea te tātai i te tāroa (t)? Wehea te 6 ki te ōwehenga whenu (cos) o te 62°. Arā te tātaitanga:
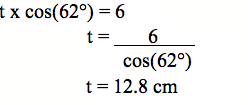
Hoatu he rapanga pēnei i tēnei, hei whiriwhiri mā te ākonga i te tāroa o tētahi tapatoru hāngai.
- Whakawhitiwhiti kōrero mō te tātai i tētahi o ngā koki o tētahi tapatoru hāngai mēnā e mōhiotia ana te tāroa, me tētahi o ngā tapa poto. I konei ka whakamahia ngā pūtohu sin-1 me cos-1 o te tātaitai.
Te mahi a te pouako He tauira kōrero mā te pouako Whakamāramatia ngā tohu ‘sin-1’ me ‘cos-1’, me te whakamahinga o ēnei pūtohu o te tātaitai hei kimi i te rahi o tētahi koki o te tapatoru hāngai. Anei te tapatoru hāngai me ngā ōwehenga mō te 30°.
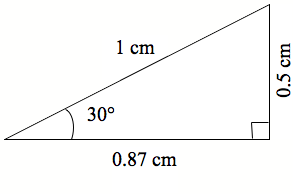
Mēnā ka whakaurua te 30 ki te tātaitai, kātahi ka pēhi i te pūtohu ‘cos’, ka puta ko te 0.8660254. Ko te 0.87 tēnei kia rua ngā mati ā-ira, te roa o te tapa pātata o te tapatoru hāngai.
Mēnā ka whakaurua te 0.8660254 ki te tātaitai, ā ka pēhi i te pūtohu cos-1’, ka puta ko te 30, koia te rahi o te koki. Arā: cos(30°) = 0.8660254 cos-1(0.8660254) = 30°
Mēnā ko te 1 cm te roa o te tāroa, ā, 0.64 cm te roa o te tapa pātata, me pēhea te tātai i te rahi o te koki (?)?
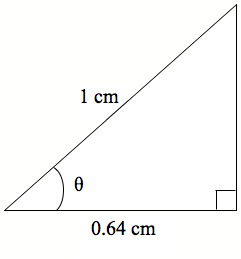
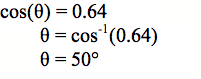
Anei anō tētahi tapatoru. E whakaaturia ana te tāroa me te tapa pātata. Me pēhea te tātai i te rahi o te koki?
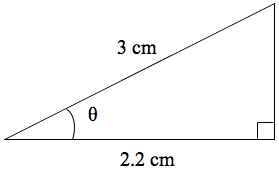
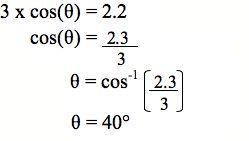
Hoatu he rapanga pēnei i tēnei, hei whiriwhiri mā te ākonga i te rahi o te koki o tētahi tapa toru hāngai. Kei Whārangi Mahi 5 (PDF, 99KB) hei tauira rapanga.
- Ko te mahi whakamutunga he whakaoti rapanga. Tuhia he rapanga ki te papa tuhituhi, ka whakawhitiwhiti kōrero ai mō te rautaki hei whakaoti. Hei tauira:
| Te rapanga | He rautaki whakaoti i te rapanga |
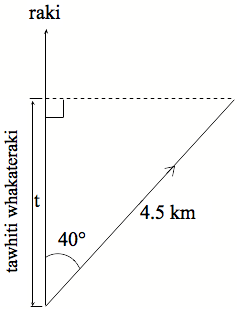
| Ko te 040° te ahunga o tētahi waka i te moana. E 4.5 km te tawhiti o te haere o tēnei waka. Pēhea nei te tawhiti whakateraki o te haere. |
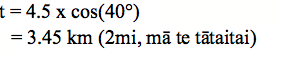 |
| Hoatu he rapanga hei whakaoti mā ngā ākonga. Kei Whārangi Mahi 6 (PDF, 87KB) he tauira rapanga. | |
Hei Whakawhānui.
Tirohia te ōwehenga pātapa (tan). Arā, te kōwae ako: www.nzmaths.co.nz