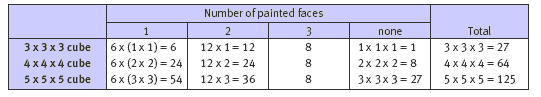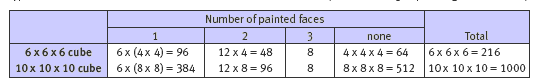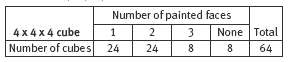Out of Sight

These three activities have been designed to help students learn to visualise 3-dimensional objects from their 2-dimensional representations and to make deductions about the hidden parts of the objects based on what they can see. Cantitowers (page 6) is a suitable activity to follow this one.

Activity
 

Before your students begin, you may need to clarify these points:

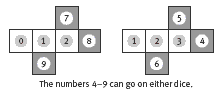
• The two cubes only show the number for the day, not the number for the month. So 1 and 2, in that order, represent the 12th day of any month.
• The cubes are fully interchangeable: the same cube doesn’t need to stay in the ones or the tens position.

If students are having difficulty, scaffold the problem by asking:

•  What numbers do you need to be able to make using the cubes? (1 to 31)
•  Which digits would you need two of, one on each cube? (1 for 11, 2 for 22)
•  How many faces are there on two cubes to put the digits on? (12)
•  If you arrange the rest of the digits on the remaining faces after you have placed the two 1s and two 2s, are there any numbers that you can’t make? (Students need to notice that 3 and 0 have to go on different cubes; the other digits can be arranged in any way. If they persist in putting the 3 and 0 on the same cube, challenge them to make the number 30 using their cubes.)

Activity Two

The key to this problem is recognising that the picture shows three views of the same cube. This means that the red and yellow faces in the illustration at left are the same red and yellow faces in the illustration at right. If students rotate view 3 in their minds one quarter turn, they will give it the same orientation as view 1 and should be able to see that the orange face is on the bottom, opposite the blue.

As a second step, students should imagine view 2 turned so that the blue face is on the top, as for view 1:

• What face is now on the bottom? (Orange)
• If we now turn the cube around (blue still on the top) so that the green and purple faces are hidden, what colours will we see on the vertical faces? (Yellow and red)
• Which of the hidden faces must be opposite the red? (Green) And opposite the yellow face? (Purple)

Many students find it difficult to visualise and rotate shapes like this in their minds. This doesn’t mean that they shouldn’t try. Let them then test their predictions by recreating the illustrations with cubes and coloured or labelled dots.

Activity Three
 

Introduce and teach these mathematical words:

If students are having difficulty with question 1, ask them:

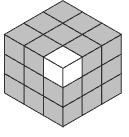
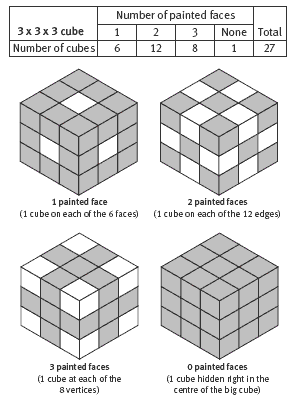
•  How many small cubes would you have if you were making Tahlia’s cube? (27)
•  This small cube (point to a corner cube) has all three of its faces painted.
• How many cubes are there like this one? (8: one at each vertex/corner)
•  Where are the cubes that have just one face painted? How many of these are there? (6: one in the centre of each face)

Have the students create a 3 x 3 x 3 cube using blocks or multilink cubes.
They can use this to check their predictions.
In question 2, help your students to make links between the 3 x 3 x 3 cube and the larger ones by asking them to explain what is special about the location of each of the 4 kinds of small cube:

• Those with 3 painted faces are always on a vertex.
• Those with 2 painted faces are always along an edge.
• Those with 1 painted face are always in the centre of a face, not touching an edge.
• Those with no painted faces are always walled up inside the large cube.

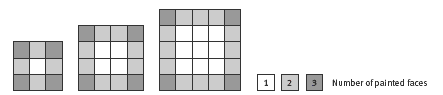
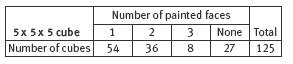
Get the students to draw one face of the 4 x 4 x 4 and 5 x 5 x 5 cubes and to colour-code the different types of painted faces, for example:

Ask the students what patterns they see developing. Key patterns are these:

•  There are always 8 cubes with 3 painted faces because every cube has 8 vertices.
•  The number of cubes with 2 painted faces is always a multiple of 12 because every cube has 12 edges.
•  The number of cubes painted on 1 face is always a multiple of 6 because every cube has 6 faces.

Encourage the students to complete their tables with this level of detail so that the patterns become clear:

Extension

Challenge your students to use the patterns they have discovered to predict the number of cubes of each type that there would be in a 6 x 6 x 6 cube or a 10 x 10 x 10 cube. (The numbers get quite large and difficult!)

Swiss mathematician, Euler (1707–1783), found a rule to describe the number of edges a 3-dimensional shape has:
f + v – 2 = e (number of faces + number of vertices – 2 = number of edges.)
Test Euler’s rule on a cube and some other 3-dimensional shapes.
After the students have completed the activities, ask these questions to promote reflective thinking:

• Today we were using information we could see to work out hidden details. Can you give me an example of this?
• What did you find difficult about imagining the parts you couldn’t see? What could you do about this?

Answers to Activities

Activity One

One of the blocks must have the numbers 0, 1, and 2 on it, and the other must have 1, 2, and 3 on it. Each of the other numbers (4, 5, 6, 7, 8, and 9) can be painted
on any of the remaining faces of either block. The diagram shows possible nets for two cardboard calendar dice. There are many ways of arranging the numbers
so that they work.

Activity Two
Orange
Activity Three
1. For a 3 x 3 x 3 cube:

2. For a 4 x 4 x 4 cube:

Compare this illustration with the one above. Can you
see patterns developing?
For a 5 x 5 x 5 cube: