The purpose of this unit is to develop understanding of the relative size of fractions. Students will also develop understanding of where fractions are located in relation to whole numbers on a number line.
- Understand and use the < and > relationship symbols.
- Recognise the relative size of unit fractions (numerator of one, e.g. 1/5).
- Recognise fractions as numbers that are positioned between, and with, whole numbers on a number line
- Recognise that whole numbers also have an infinite number of fraction names, for example, 3 = 6/2, 12/4, etc.
- Compare the size of proper fractions, improper fractions, and mixed numerals.
- Recognise that when comparing the size of fractions, as numbers, the size of the whole is kept constant.
Fractions are an extension of whole numbers and integers. The symbols for fractions comprise two whole numbers separated by a vinculum (bar): one on the top (numerator) and one on the bottom (denominator). Consider four fifths (4/5) . The numerator, four, is a count of how many equal parts the fraction is made from. The denominator, five, tells the size of those parts with reference to the size of one whole. Fifths are made from partitioning one whole into five equal parts.The unit of one can be a continuous whole, such as a shape or a container of liquid, or a set containing units of one. The latter model is more complex to deal with.
Fractions are needed when wholes (ones) are not adequate for a task. This is often evidenced in division which often requires the equal partitioning of ones. Sharing two chocolate bars (2 wholes) equally among five people requires that the bars be cut into smaller equal parts. The operation might be recorded as 2 ÷ 5 = 2/5. Note that the number two fifths, is composed of two units of one fifth. In practical terms the equal share can occur by dividing each of the two bars into fifths, then giving each person one fifth from each bar. The need for fractions is also evidenced in measurement. Consider the context of measuring height. Metre lengths are the whole (ones) in this expression of quantity. However, your height might be 1.78 metres. Whilst whole metres may be inadequate as a unit for measuring your height, equal parts of metres can be used to achieve greater precision. Note that the presence of fractions in measurement is often masked by the use of decimals.
Any fraction can be expressed as an infinite number of equivalent fractions that represent the same quantity. For example, if the bar of chocolate was made up of ten pieces then each person might be given two tenths from each bar, giving them four tenths in total. Four tenths (4/10) are the same quantity of chocolate as two fifths. Since 4/10 and ⅖ are equivalent fractions (i.e. representing the same quantity) they occupy the same position on a number line. There are an infinite number of fractions that can occupy that same position.
Once students understand the equivalence of different fractions, they are able to add and subtract fractions with common denominators. Addition and subtraction require quantities that are expressed in the same unit. This is simple with whole numbers, as quantities are always expressed using units of one. However, with fractions, the units can be different (e.g. 2/5 + 1/2 = ?) Two fifths are made up of two units of one fifth. These are different in size to halves. A standard method is to rename the fractions, so they share a common denominator. Two fifths is equivalent to four tenths (2/5 = 4/10) and one half is equivalent to five tenths (1/2 = 5/10) Since four tenths and five tenths share the same unit(tenths) they can be combined to make nine tenths (4/10 + 5/10 = 9/10).
The properties of addition and multiplication that hold for whole numbers also hold for fractions. To find a fraction of another amount is to treat the fraction as an operator. For example, three quarters of 24 is represented symbolically as 3/4 x 24, with three quarters operating on 24 as a multiplier or scalar.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate the tasks include:
- varying the level of abstraction. Materials, mostly paper strips and circles, are used throughout the unit as physical references. Encouraging students to experiment to find out what happens with quantities, and to generalise what happens, is the first step towards abstract thinking. Through predictive questioning encourage students to reason with diagrammatic representations and symbols, noting relationship among the parts of fraction symbols.
- altering the complexity of the numbers involved, or the relationships between numerators and denominators. Fractions that involve repeated halving, such as halves, quarter, eighths, etc., are much easier to work with than other fractions. Thirding, fifthing, seventhing, etc., are more complicated as the relationships between numerators and denominators are more complex, e.g. 2/3 = □/21.
- providing opportunities for small-group teaching to further scaffold ākonga in need of more support
- providing opportunities for more knowledgeable ākonga to apply their understanding and write questions for peers to solve
- allowing use of scientific calculators that can process fractions. Do so in a predictive way. Ask students to anticipate the result of a physical action or symbolic manipulation, then confirm the result with a calculator. If the prediction disagrees with the calculator answer, find out why that occurs. Students benefit by folding back from symbolic answer to a physical model. Calculators are also useful for establishing patterns in symbolic forms, e.g. How much bigger is 3/4 than 2/3? (Try 3/4 - 2/3 = on a scientific calculator.)
Adaptation involves changing the contexts used for problems to meet the interests and cultural backgrounds of your students. Where contexts such as food may not be appropriate for your students, find other situations likely to engage them. For example, instead of an apple, clay or a piece of paper could be used. And instead of beans, shells or stones could be used. Points earned on a computer could be reframed as points earned in a Kapa Haka performance or basketball game. Pizzas might be reframed as rounds of totara, hard drives of a computer, or areas of a kamo kamo patch. You could also choose a context that reflects current learning from another curriculum area.
Te reo Māori vocabulary terms such as hautau (fraction), tūtaha (whole), and haurua, hautoru, hauwhā… (half, third, quarter…) could be introduced in this unit and used throughout other mathematical learning.
- An apple or plasticine/modelling clay
- Plastic knife
- Counters
- Paper strips
- Glue sticks
- Scissors
- Two coloured pegs
- Plastic beans
- Poster paper
- Blank dice
- Commercial fraction sets; strips and circles (optional) and/or access to interactive tools.
- Screen display or Interactive whiteboard
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- Copymaster 7
Session 1
The purpose of this session is to consolidate understanding of fraction symbols, to introduce the < and > relationship symbols, and to explore the relative size of unit fractions. Students will also consoilidate their understanding that the more pieces (parts of regions) something is cut into, the smaller the pieces.
Activity 1
Begin by playing Fraction Bingo (Copymaster 1) to consolidate recognition and correct reading of fraction symbols.
Give a Player bingo card and 10 coloured counters to each student in the group/class. The nominated caller reads out Caller clue cards, and students cover the matching number on their card with a counter. The first player to fill their card calls “Bingo”.
Activity 2
- Take one apple (or piece of bread, wrap, etc.), cut it and share it equally between two students. Have each student cut their half in half so everyone gets an equal share.
What fraction of the apple is each person getting now? (one quarter)
How is one quarter written in numbers? (1/4) - Ask each of the four students to invite another friend each and cut their quarter in half again (eighths). Repeat once again (sixteenths). Predict what would happen if the process repeats once more (thirty seconds).
- Discuss what is happening to the number and size of the pieces as the repeated halving happens. Ask a student to record the fraction names for one that are made.
2/2 4/4 8/8 16/16 32/32
What is the same about all these numbers for one (whole) apple? - Ask the students to discuss in pairs what is happening and generate a summary statement to record on a class chart. For example: ‘The more pieces that one (thing) is cut into the smaller the fractions will be. As the fractions get smaller the denominator (number of parts) gets bigger.’ Consider pairing students with mixed levels of confidence and mathematical knowledge to encourage tukana-teina (peer learning).
Activity 3
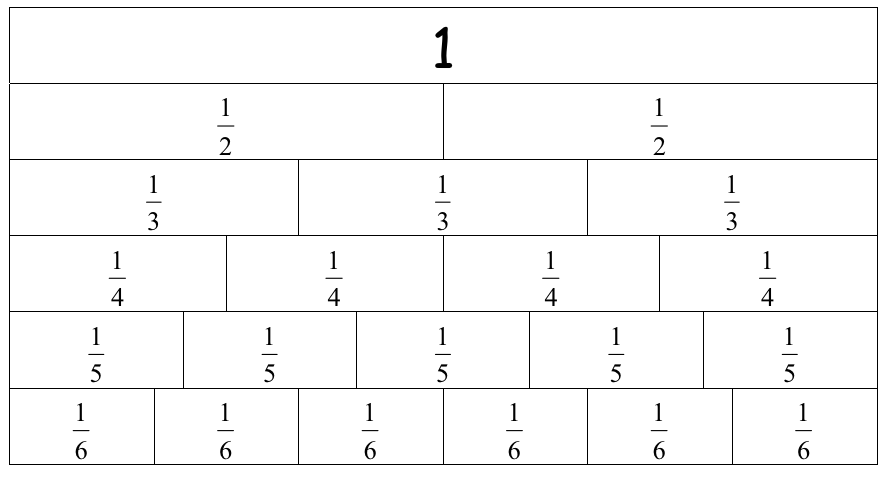
- Begin with a discussion around when students have used fractions (e.g. cooking, building, sport). Explain to them that you are going to look at and compare the sizes of different fractions. Provide students with strips of paper that are the same length. Cutting A4 paper longways works well. Challenge the students to fold a single strip into halves, quarters, eighths, thirds, fifths, and sixths. Ask them to label the pieces, e.g. 1/4 on all the quarters. You could let students do this independently, or begin with more structured peer-work. Ensure your students understand which direction they need to fold the paper in.
- Ask equivalence questions such as:
How many eighths are the same length as one half? - Ask composition questions such as:
With your strips, how many ways can you make one half? - Ask partitioning questions such as:
How would you fold twelfths? - Distribute Copymaster Two to pairs of students.
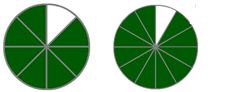
- Ask each pair to cut out a unit fraction strip, that is one piece with a particular denominator, e.g. 1/5 or 1/8.
- Gather the students in a circle on a mat space. Have a one copy of Copymaster Two, and a copy of each unit fraction strip available for reference. Ask the students to place their strip in the centre face down. Mix the strips up. Ask students to guess the fraction of each piece.
How can we use the one strip to check your guess?
Students should note that the number of times the given strip fits in one reveals the fraction, e.g. “Five of this strip will fit into one so the strip is one fifth.” - Order the fraction pieces from smallest to largest, arranging them vertically with a common baseline. Use the arrangement to create a fraction number line.
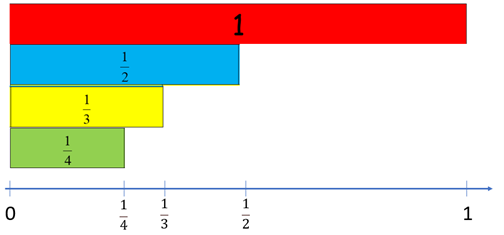
Draw attention to the fact that the smallest fraction (1/20) is the closest to zero.
Name a fraction that is smaller than one twentieth.
Could a unit fraction be equal to zero? The larger the denominator of a unit fraction is, the closer it is to zero (the pieces become smaller and smaller). Any fraction with zero as the numerator (for example 0/2) equals zero, however these are not unit fractions.
Activity 4
- On the class chart write the ‘is greater than’ symbol: >. Discuss this symbol.
What does this symbol mean? - Discuss the equals symbol, = . Both lengths are the same and the space between them stays the same, which is the meaning of equality. The > symbol must mean an inequality, the number on the left is greater than the number on the right. You might use the traditional ‘Crocodile’s mouth’ story or song (available online) to help students remember the direction of the sign. The greedy crocodile always tries to eat the larger number.
For example, the relationship between 4 and 5 might be expressed as 5 > 4, meaning “five is greater than four” when the expression is read from left to right. - Repeat with the ‘is less than’ symbol (<). Emphasise that each of these symbols (=, >, <) expresses a relationship between the two numbers on either side of the symbol. For example: 6 is greater than 4 can also be written 6 > 4, 6 is the same as 6 is also written as 6 = 6, and 4 is less than 6 can also be written 4 < 6.
- Write some fraction pairs on the board and ask students to put the correct symbol showing the relationship between the numbers. Include some simple equivalent fractions for equality. For example:
1/5 1/10
1/3 1/2
2/4 1/2
Encourage ākonga to use their fraction strips and the class copy of the fraction wall (Copymaster Two) to support their thinking. Students ready for extension could make up further fraction pairs problems for a partner to solve.
Session 2
The purpose of this session for students to consolidate their understanding of the relative size of fractions and to recognise fractions as single numbers, even though they are composed of two whole numbers. The session also looks as ‘density’ of fractions on the number line. Whole numbers can be expressed as fractions and fractions are located between whole numbers.
Activity 1
Introduce this session by adapting Squeeze - Guess My Number with whole numbers on a number line.
A peg is put at each end of a number line, for example, on 0 and 100. A student chooses a number between the pegs and writes it on a piece of paper. The rest of the students ask “less than” or “greater than” questions to find the mystery number. With each question, a peg is moved to eliminate numbers.
For example, if “Is it greater than 25?” is answered by “Yes”, then the zero peg is shifted up to 25 to eliminate all the numbers 25 and under. If “Is it less than 75?” is answered by “Yes”, then the top peg is shifted down to 75 to eliminate all the numbers 75 and over.
This continues until the mystery number is finally found by squeezing in from above and below.
Activity 2
- Draw a number line from zero to five including an arrow at each end (meaning the line extends infinitely in each direction).
Write 1/2 on the board.
What is this number?
Where does this number fit on our number line? - Have the students discuss the location of one half in pairs, agree on their decision, then have one student come up and show where 1/2 is located. There may be incorrect ideas. For example, some students may suggest the one half is between two and three because it is halfway along the space between 0 and 5. Those students are locating the number that is one half of five.
Correct (One half as a number)
Incorrect (One half as an operator on five)
What number is one half of five? (2 ½) - Locate, and agree that 1/2 is halfway between 0 and 1.
- Explain to the students that they are going to ‘magnify’ this section between zero and one (0-1) of the number line. Students will create their own fraction number line.
- Distribute several paper strips to each student, made by cutting A3 paper lengthwise.
Ask students to draw a line on their strip, as shown, and mark 0 and 1. Refer back to the whole number line, highlighting the fact that their strip is the 0-1 section magnified.
- Ask your students to cut several strips that are ‘one long.’ That is the length between zero and one on their number line.

- Discuss how students might fold a one strip into thirds.

Where do we mark one third and two thirds on our number line?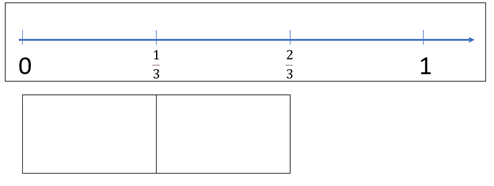
- Ensure students understand that the location of one third is at the endpoint of a one third length, and that two thirds is marked at the endpoint of two thirds lengths joined (iterated).
Where should we mark three thirds? (Do students recognise that 3/3 is the same length as one?) - Repeat the same process with halves, quarters, and fifths, adding fractions to the number line each time. Students should end up with a number line like this:

- Pose problems about the size relationship of the fractions. For example:
Which fraction is greater two fifths or three fifths?
Why are three fifths greater than two fifths?
How could we record that relationship using an equals, greater than, or less than symbol? (2/5 < 3/5)
Good comparisons for students to explore are:
Three quarters and three fifths
One third and two fifths
One half and two quarters
Three fifths and two thirds - Do students recognise that the size comparison cannot be made only by looking at the numerators, or denominators separately? Both the number of fraction parts (numerator) and the size of the parts (denominator) need to be considered.
- Ask: Where would these fractions go on your number line?
Write 2/2, 3/3, 4/4, 5/5 on the board.
Do students recognise and can explain why these fractions are all names for one (whole)? - Write the fractions 1/18, 1/20, 1/80, 1/100 and ask students to discuss where these fractions would be located. (to the left of 1/8 and to the right of zero).
Where is 1/1000 located? (recognising that such a fraction would be too small to see on this number strip, as it is so close to zero. You might discuss a millimetre as 1/1000 of the length of 1 metre) - Expand this discussion to include the ‘infinitely small’ as appropriate.
- Ask students to label each fraction strip piece and store the pieces for the next lesson.
Activity 3
Draw a number line from zero to one on the board.
Play Squeeze - Guess My Number on this newly created class fraction number line. Specify that the only fractions permitted are those you have used in Activity 2, halves, thirds, fourth (quarters) and fifths. Questions must involve fractions, e.g. “Is the number greater than one half?”
After some whole class games let students play the game in pairs.
Activity 4
- Have the fraction number strip 0-3 from 2 and 3 above visible to the students. Using fraction circle pieces, show the students a regional representation of two thirds and of three quarters.
Write on the class/group chart:
“Which is closer to one, 2/3 or 3/4? Why?” Or “Which is near to making one whole circle, two thirds or three quarters? Why?”
Have the students discuss in pairs and come to an agreement on the answers to both parts of the question.
Share and discuss. (For example: “The more pieces there are, the smaller each piece is. As the denominator gets bigger, the smaller just one missing piece will be.”)
- Write on the chart 11/12 and 7/8. Ask them to picture these, agree on which is closer to one and explain why. Show the region representations and discuss further.
Activity 5
Ask students to work in pairs (tuakana-teina) to make a poster or digital display, with words, diagrams and symbols, explaining what they have learned in Session 2 about ordering fractions. If some students require consolidation working with quarters, halves, and thirds, work with them in a small group - repeating the activities in this lesson in a more structured manner.
Ensure that students understand that their own classmates will be the audience for their posters and that the posters are to be displayed on the maths wall space.
See also the Trains activity from Numeracy Book 7.
Session 3
The purpose of this session is for students to consolidate their understanding of the relative size of fractions and where they fit with whole numbers on a number line. Students are formally introduced to improper fractions and mixed numerals.
Activity 1
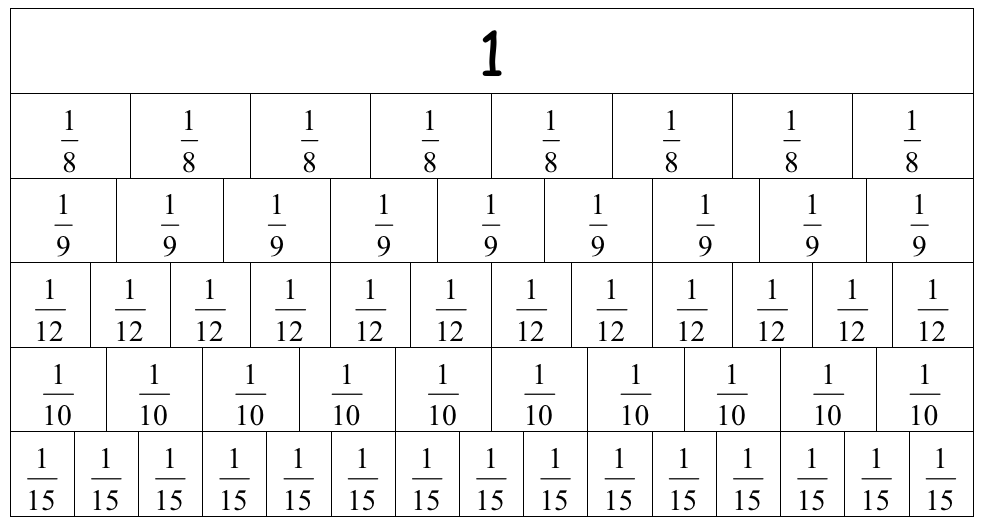
- As consolidation, students follow the steps above to create eighths strips and record the iterations of one eighth, 1/8, 2/8, 3/8, …8/8 on their number line.
Were some of the fractions the same size as fractions you already had?
Which fractions were equivalent to others? Why were they equal to the same amount?
Do students realise that eighths are half the size of quarters so each length of two eights is the same as one quarter?
Do they recognise four eighths as the same as one half?
Do they recall that 8/8 is the same as other names for one, such as 2/2, 3/3, 4/4, etc. - Create a fraction number strip from zero to five, ensuring that the iterations of one match the length of a one strip from the last lesson.

- Locate these fractions on the number line:
9/8, 6/4, 5/2, 12/3, 24/5 - Discuss the meaning of each fraction with particular emphasis on:
The numerator (top number) is a count of how many equal parts are joined.
The denominator (bottom number) gives the size of the parts, how many of the parts make one. - If needed, physically place strips one after the other to correctly locate each fraction. For example:
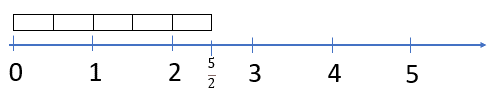
What might we look for in the fraction to help us work out how big it is?
Do students consider how many of the denominator parts make one?
For example, three thirds make one, so six thirds make two ones, and nine thirds make three. 12 ÷ 3 = 4 so twelve thirds equals four ones (4). - Give each pair of students a long strip of paper and ask them to create a number line from zero to five. Tell them to use the fraction lengths to make a fraction number line. Use the same unit fractions on each line, quarters, thirds, fifths, or eighths. An example of a finished number line might be:

- Display the number lines and have students count aloud in fractions of equal parts, taking turns around the group. For example: “one half, one, one and a half, two, two and a half, three….”, or “one eighth, two eighths, three eights...”
Have one student place a transparent coloured counter, or peg, on each of the fraction numbers as the counting proceeds. Be sure to also count backwards with counters being removed accordingly. For example: 5, 4 1/2, 4, 3 1/2, 3…
Try also counting forwards or backwards in quarters and leave the pegs in place.
Activity 2
- Pose this problem to your students:
Hattie eats six quarters of a submarine sandwich.
Peri eats eight fifths of a submarine sandwich.
Fali eats five thirds of a submarine sandwich.
Each ‘sub’ is the same length.
“Eight pieces is more than six or five,” says Peri, “I ate the most.”
Is Peri right?
If possible, adapt the context of this problem to reflect a context that is relevant to your students (for example, number of children racing in Dragon Boats, area of the school garden to be planted). - Let students use their fraction pieces to solve the problem or work more abstractly if they want. Encourage them to justify their answer and to record the argument they will make in support of that answer. Look for strategies like building the fractions with the same baseline (zero) and compare the lengths.
Some students might recognise that all three fractions are improper. That means the numerators are greater than the denominators. Therefore, each fraction is greater than one and can be renamed as a mixed number, e.g. 5/3=1 2/3. - Gather the class to share solutions.
Why does Fali eat the most submarine sandwich when he has the smallest number of pieces?
Why does Peri eat the greatest number of pieces but still not eat the most sandwich?
How could each fraction be written in another way? (6/4 = 1 2/4 = 1 1/2, 8/5 = 1 3/5, 5/3=1 2/3)
Does writing the fractions as mixed numbers help to solve the problem? - Ask your students to make up comparison problems with improper fractions for their classmates to solve. Share the problems and make a display, or book of problems.
Activity 3
Let students play Stars to Mars: Fractions in order using Copymaster Three to practise concepts of fraction order, mixed numerals, and improper fractions.
Session 4
The purpose of this session is to consolidate students’ understanding of the proper fractions, improper fractions, and mixed numerals. For this lesson students will need Copymaster Four: Fraction Circle Pieces.
Activity 1
- Begin by building non-unit fractions with circular fraction pieces. You might use a commercial set of pieces, coloured, laminated and cut-out versions of Copymaster Four, or an online tool (Search “Fraction Circle Interactive”).
For example, construct 2/3 and 1/2 Remind students that the numerator is a count of the number of parts. Record the symbols.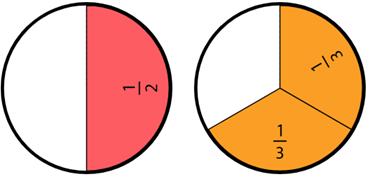
Which fraction is larger? How can we show this with symbols? (i.e. <>)
How can this be true when halves are larger than thirds?
How can the relationship be recorded using mathematics symbols? (1/2 < 2/3, or 2/3 > 1/2)
How much greater is two thirds than one half? (One sixth)
Why is the difference between the two fractions equal to one sixth?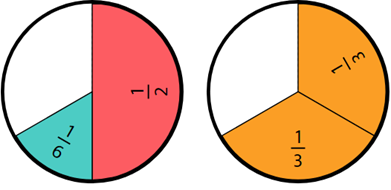
- Pose other similar problems with increasing difficulty following the same sequence of questions
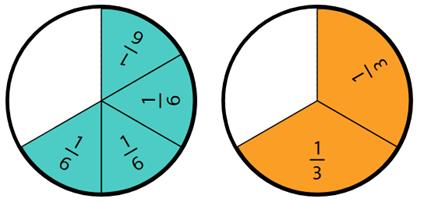
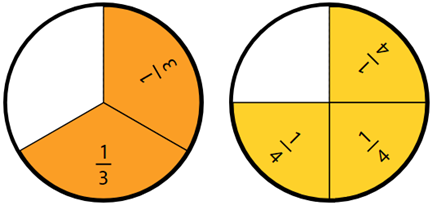
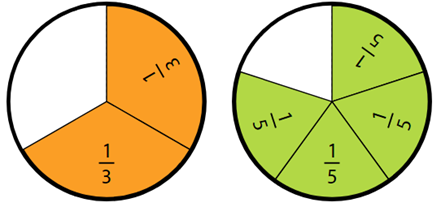
- Is there a way to look at the fraction symbols and tell which fraction is greater without having to create pictures?
Use the example of 5/8 and 3/5.
Which fraction has the most pieces or parts? (5/8)
What fraction has the largest pieces or parts? (3/5)
Ask students to predict which fraction is greater. Look out for ‘gap thinking’ such as 5/8 is three pieces from one, and 3/5 is two pieces from one, so 3/5 is larger (incorrect in this case). Look for students to consider the size of both numerator and denominator. They might consider using benchmarks such as one half.
“Five eighths are an eighth bigger than one half, and 3/5 are half a fifth bigger than one half, one tenth. Therefore, five eighths are bigger.” - Provide the students with Copymaster Five to complete in pairs. Students might also need sets of fraction circle pieces (Copymaster Four), or access to an online tool.
As they work, look for students to:- Correctly name each fraction in the pair and express the fractions with symbols.
- Consider the importance of both numerator and denominator in determining the size of a fraction.
- Compare the image of the fractions with their thinking and justify their answers, particularly their judgement of “how much more.”
- Gather the class and share answers. If any students use equivalence, highlight their work, and ask them to explain their strategies. For example, problem f compares 4/6 and ¾. Both fractions can be renamed as twelfths, twenty fourths, etc.
4/6 = 8/12 and 3/4 = 9/12. Therefore, 3/4 is one twelfth greater than 4/6. This relation might be recorded as 3/4 - 4/6 = 1/12 (difference).
Activity 2
- Pose this riddle to your students.
I am a fraction.
I am greater than one half but less than one.
What might I be?
You might record the riddle like this: ½ > ? < 1. Let students suggest some possible fractions such as two thirds, three quarters, and 7 eighths. - Record their suggestions using symbols: 2/3, ¾, 3/5, 4/5, 7/8.
What is the same about these fractions?
Some students might recognise that the numerator is more than half the denominator but not equal to the denominator. - Reveal another clue:
If you add one tenth to the fraction you make one.
What fraction am I?
Students might need to work with their fraction circles to establish the mystery fractions. They might reason that ten tenths make one, so nine tenths is the fraction that is one less than one. - Pose other riddles for the students to solve such as:
I am a fraction between one quarter and one half.
My numerator is three.
What fraction might I be?
Answers are 3/7, 3/8, 3/9 (1/3), 3/10, 3/11
I am a fraction that is close to one half.
My denominator is twelve. - What fraction might I be?
Depending on what is considered close, answers are 5/12 and 7/12.
Why can’t the fraction be 6/12? - Ask your students to make up a fraction riddle for someone else to solve.
Activity Three
- What is the same about these fractions?
1/2 2/4 3/6 4/8 5/10 6/12
Do students recognise that these fractions all equal one half?
If one half was cut into ten equal pieces what would the pieces be called? (Twentieths)
How many twentieths equal one half? (10/20)
How many hundredths equal one half? (50/100) - Use other fractions as starters. For example:
Find as many fractions as you can that equal 3/4, or 2/5, or 1/8.
Session 5
In this session students transfer their knowledge of equivalent fractions to the sets model. This setting is more difficult than settings with a fixed one unit as the whole is composed of a collection of ones, and fractions are found in the ratio between the number of items in a part and the whole.
Activity 1
- Begin the lesson by reading together conclusions drawn in Session 3 in which the students worked with a linear representation (number line).
- Explain to the students that they will be working with proper fractions, improper fractions and mixed numerals in the context of sets of beans.
Have student pairs each take a sizeable handful of coloured beans between them and make writing material available.
Write the following (or something similar that better reflects the interests and cultural knowledge of your class) on the class chart:
In Jack’s Garden Shop beans come in packets (or sets) of six. Write a mixed numeral showing how many packets Jack could make with the beans you have. - Ask a pair of students to record their mixed numeral on the class chart and have them explain how they worked the fraction out.
- Record their explanation: For example:
Joe and Manu took 23 beans. They wrote correctly 3 5/6 . “We made groups of six out of the beans. That was three packets and 5 beans left. Each bean equals one sixth of a whole packet, so five beans are five sixths of a packet. We wrote 3 and 5/6.”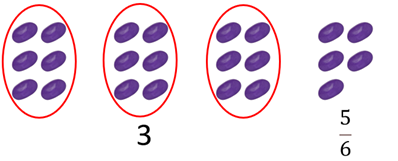
- Ask the students to write the improper fraction that has the same value as the mixed numeral. (In Joe and Manu‘s case it’s 23/6)
- Repeat this process with several pairs of students. Ask the student pairs to write an explanation of how to change an improper fraction (23/6) to a mixed numeral (3 5/6). Discuss and record their suggestions.
- Summarise formally by concluding that the numerator is divided by the denominator. The quotient (answer to division) names the whole number part and the remainder gives the fraction of a set.
- Let’s change the packet size to three beans. What effect does that have on the number of packets you have?
Can the students reunitise? Reunitising involves thinking with a whole of three, not six beans? Some students may realise that halving the packet size doubles the number of packets that can be made from a given number of beans. For example, consider 23 beans, as above. 2 × 3 5/6 = 7 2/3 since 10 sixths equals one and two thirds.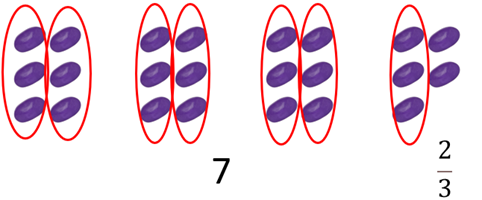
- Explore the effect of changing packet size on the number of packets that can be made.
- Provide the students with copies of Copymaster Six. Ask them to solve the problems then share their solutions with a partner. Note that the unknown is varied in each question set.
Activity 2
- Make beans available to the students should they need to use them. Pose several problems in which the fraction of the set (part) and total number of beans is given. Students need to work out the number in a set (whole) and the number of sets the total of beans will make, recording this as a mixed numeral.
For example: 3 beans is 1/3 of a packet. How many packets can be made with 17 beans? If 1/3 is 3 then 3/3 is 9. 17/ 9 is 1 8/9. - Pose further problems such as “2 beans is 1/6 of a packet. How many packets can be made with 17 beans?” or “4 beans is 1/4 of a packet. How many packets can be made with 17 beans?” or “5 beans is 1/2 of a packet. How many packets can be made with 17 beans?”
Have students pair share their results, explaining their methods. - Have students make up problems for their partner to solve.
Activity 3
Use Copymaster Seven to make three different co-operative logic puzzles (Easy, Medium, Hard). Students should solve the problems in groups of four. Two players get two clues each, and the other two players get a single card. Each clue must be satisfied for the answer to be correct. Each group will need access to beans or some other form of counter. Some students may be able to complete the puzzle without material support.
The answers are: 18 (Easy), 25 (Medium), 42 (Hard)
Dear parents and whānau,
In mathematics this week we have been comparing and ordering fractions according to their size. Your child would like to challenge you to a game called Stars to Mars that we have been playing in class. We hope you enjoy it.