Use a range of strategies to solve problems that involve a combination of addition, subtraction, multiplication, and division.
Number Framework Stage 7
Calculators
Order of Operations (Material Master 8-5).
Scientific calculators and spreadsheets produce correct answers to multiple-step calculations as they are programmed to follow the correct conventions. Some care is required with these conventions. For example, there is a “left to right” convention to work out 12 – 4 – 6 giving 2 whereas 12 – (4 – 6) overrides this convention to produce 14. This needs careful teaching.
Using Number Properties
Problem: “Julia’s simple calculator works out 8 + 3 x 6 and gets 66. Maree works out 8 + 3 x 6 on a scientific calculator or a spreadsheet and gets 26. Discuss why the answers are different.”
(Answer: Simple calculators work from left to right through a multi-stepped calculation. So 8 + 3 produces 11 on screen, then x 6 gives the answer to 11 x 6 which is 66. But scientific calculators and spreadsheets are programmed to do the multiplication first. So for 8 + 3 x 6, they work out 3 x 6 first to get 18. Then they work out 8 + 18 to get 26.)
Problem: “Potatoes cost $0.91 per kilogram. Julia buys 3.456 kg of potatoes on Monday and 2.087 kg of potatoes on Tuesday. She writes the cost down as 3.456 + 2.087 x 0.91.
Why will this not be correct on a scientific calculator?”
(Answer: The addition needs to be done first in this problem.)
Discuss the effect of brackets. Write 3.456 + 2.087 x 0.91 on the board and add brackets. (Answer: (3.456 + 2.087) x 0.91.)
Get the students to enter the numbers and brackets on a scientific calculator or spreadsheet and get them to answer to the nearest cent. Discuss whether the answer is correct. (Answer: It is correct. Brackets override the “times before add” rule.)
Problem: “Work out (2 + 3 x 4) x 2 without a calculator.”
Discuss the convention that brackets are calculated first, and within brackets, the times before add convention is obeyed. (Answer: (2 + 3 x 4) x 2 = (2 + 12) x 2 = 14 x 2 = 28.)
Problem: “Work out (2 + 6 ÷ 3) _ 2 – 14 ÷ 7 without a calculator.”
Introduce the convention that, while brackets are still calculated first, within brackets, multiplication/division precede addition/subtraction. (Answer: 6.)
Teaching Number Sense and Algebraic Thinking
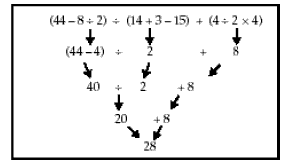
Problem: “Work out (44 – 8 ÷ 2) ÷ (14 + 3 – 15) + (4 ÷ 2 _ 4) without a calculator.”
Introduce the convention that, within brackets, if the operations are only + and –, work through the bracket from left to right because + and – are equal in importance.
Similarly if the bracket contains only x and ÷, work left to right through the bracket as x and ÷ are equal in importance.
Examples: Worksheet (Material Master 8–5).