This problem solving activity has a number and algebra (equations and expressions) focus.
The farmer is putting a new chicken run up against a brick wall.
He has 20 metres of wire to put round the run.
If he makes a rectangular run, how big an area can he enclose?
- Use algebraic equations to determine the maximum area of a rectangle with a given partial perimeter.
This problem challenges students to maximise an area given a number of parameters. The method of finding two equations and eliminating one of the variables is one that is often used in maximum and minimum problems in calculus.
To solve this problem students must be able to measure lengths and calculate areas of rectangles using the formula: area = length x width, and to apply an elementary knowledge of parabolas. It would also be an advantage if they have used a table and applied algebra to find solutions to the problems. This could be further explored with the problems Peter’s Second String, Measurement, Level 5 and Peter’s Third String, Number and Algebra (Equations and Expressions), Level 6.
Mathematics is more than doing calculations or following routine instructions. Thinking and creating are at the heart of the subject. Though some problems have a set procedure or a formula that can be used to solve them, the most worthwhile problems require the use of known mathematics in a novel way.
There are seven problems related to perimeter and area.
The first set includes: Peters’ String, Measurement, Level 4; Peters’ Second String, Measurement, Level 5; Peters’ Third String, Number and Algebra (Equations and Expressions), Level 6; and Polygonal String Problem, Number and Algebra (Equations and Expressions), Level 6. These show the non-link between rectangles’ areas and perimeters, including showing that among all quadrilaterals with a fixed perimeter, the square has the largest area. The final problem explores the areas of regular polygons with a fixed perimeter and shows that they are ‘bounded above’ by the circle with the same perimeter.
The second set includes: Karen’s Tiles, Measurement, Level 5; and Karen’s Second Tiles, Number and Algebra (Equations and Expressions), Level 6. These problems explore maximum and minimum perimeters for a given area.
The Problem
The farmer is putting a new chicken run up against a brick wall. He has 20 metres of wire to put round the run. If he makes a rectangular run, how big an area can he enclose?
Teaching Sequence
- Introduce the problem to the class. Have them consider how they might approach it.
- Let the class investigate the problem in any way that they want. Make string available to those who want to model the situation.
To use a table they will have to find some equations. Provide support for this as necessary. - Check on groups' progress as they work. Encourage students to set up equations and reduce the number of dependent variables to one.
- If a number of students are struggling, a brainstorming session may help.
- Share and discuss the students’ answers. Have them to write up their work, making sure that they have carefully explained their arguments.
- Encourage students to attempt the Extension Problem.
Extension
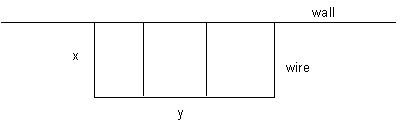
The farmer wants to have some ‘rooms’ in the chicken run to separate some of the hens. So he uses the 20 m of wire slightly differently.
See the diagram. What is the biggest area that he can contain now?
Solution
This solution is the most sophisticated available to the students at this point of time.
In the diagram below, the variable x is the distance that the run is from the wall, and y the length of the run.
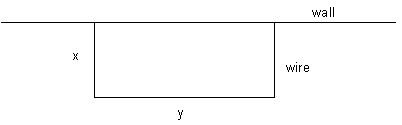
Set up some equations. First we know that the length of the chicken wire is 20 m. But it is also equal to x + y + x. So 2x + y = 20 … (1).
Then we know that the area, A, of the chicken run is xy. So A = xy ... (2)
Eliminating y from (1) and (2) gives A = x(20 – 2x). At this point we are in exactly the same situation as we were in Peter's Third String, Level 6.
We have a parabola. Its maximum point is halfway between x = 0 and x = 10 (where 20 – 2x = 0). So the maximum is at x = 5. When x = 5, A = 50. So the maximum area is 50 m2.
Note: 1. This problem can be solved using a table as in Peter’s Second String, Level 5. It can also be solved using Calculus but that seems to be an unnecessarily complicated way to solve it.
2. The answer to this problem is not a square. The chicken run of maximum area does not have x = y.
Solution to the Extension
.gif)
The two equations we get this time are 4x + y = 20 and A = xy. Eliminating y now gives the equation A = x(20 – 4x). This parabola has its maximum point halfway between x = 0 and x = 5. So the maximum is at x = 2.5, where A = 25 m2.
