This problem solving activity has a geometry focus.
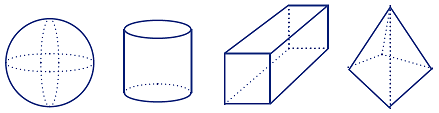
Eva, Tamati, Noah and Jo are looking at these shapes.
Eva says, "Hey, the first shape is the odd one out."
Tamati says, "No, Eva, the second one’s the odd thing out!"
Noah says, "No, it’s the third one!"
Jo says, "Well you are ALL wrong! The last one is clearly the odd thing out."
Who is right and why?
- List a number of properties that distinguish the 3-dimensional solids of the problem.
- Devise and use Problem Solving Strategies to explore situations mathematically, in particular guess and check, draw a picture, and use equipment.
This problem explores basic properties of 3-dimensional figures including symmetry, and number of sides (flat surfaces), lines (edges), and corners (vertices). It’s important for students to recognise basic properties of common solid figures so they can build on and refine these as they learn more. Important fundamental language of geometry is established as they correctly name and describe each figure.
There is no correct answer to this problem. Students may suggest several ideas that are not listed in the solution. Discuss these as they arise.
The Level 1 Geometry problem, Odd One Out is a problem very similar to this.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Enough spheres, cylinders, cuboids, and square-based pyramids for the class to use.
The Problem
Eva, Tamati, Noah and Jo are looking at these shapes.
Eva says, "Hey, the first shape is the odd one out."
Tamati says, "No, Eva, the second one’s the odd thing out!"
Noah says, "No, it’s the third one!"
Jo says, "Well you are ALL wrong! The last one is clearly the odd thing out."
Who is right and why?
Teaching Sequence
- Show, discuss and have students name the four given shapes. Discuss the type of shape (3D) and what shapes are used to form the faces of the shape (e.g. 2D shapes - square, circle etc.) Draw attention to key vocabulary terms: face, edge, corner, symmetry.
- Read the problem together. Have some students summarise what the problem is asking them to find out.
- Discuss how they might approach the problem and record their solutions. Agree that one useful way to present the information is to write it in a table.
- As students work on the problem in groups or on their own, ask questions that support them to consider the different attributes of the shapes.
How many faces does this shape have?
What other shapes can you see that are a part of this shape?
What would this shape look like if you cut it in half? Would the halves be symmetrical? This could be explored with a digital representative or play dough.
How many corners does this shape have?
How many edges does this shape have? - Have students present their ideas. As they do so, record these on a class table that can be added to over time.
- Discuss the extension problem.
- At this point or as a follow-up activity you might put one of the objects in a feely bag. Ask a students to put a hand in the bag and then tell the class what they feel. Warn the student that they are not to tell the class what the object is but rather what properties they can feel. The class should try to guess what the object is that the student is describing.
Extension
Ask the students to find other 3-dimensional objects in the classroom. Get them to say what makes them different from each other and from the four objects of the original problem.
Solution
There are multiple solutions to this problem. Eva is right because the sphere will roll no matter how you put it on the ground. Tamati is right because the cylinder is the only one that has a flat face and a curved face. Noah is right because the box is the only object that has six faces. Jo is right because only the pyramid has five faces.
Challenge the class to give as many reasons as they can to explain why each object is really the odd man out.
sphere | cylinder | cuboid (box) | square pyramid |
rolls no matter how you put it down | has curved and flat faces | has 6 faces | has 5 faces |
any diameter is an axis of rotational symmetry | has circular faces | has 4 rectangular faces | has 4 triangular faces |
could play netball with it | any cross-section parallel to a face is a circle | any cross-section parallel to a rectangular face is a rectangle | has a vertex where 4 faces meet |
… | has two edges but no vertices | has 12 edges | has 8 edges |
… | … | has 8 vertices | … |
Add to the table as different properties of the given objects emerge and as further shapes are explored and compared.