Odd One Out
list a number of properties that distinguish squares from circles from cubes from pentagons.
devise and use problem solving strategies to explore situations mathematically (guess and check, make a drawing, use equipment).
This problem aims to explore basic properties of shapes. These properties include their symmetry and colour. It is important for students to get a good feel for shapes so that they can delve deeper into their properties and uses later on.
There is no correct answer to this problem. It is likely that the students will come up with several answers that we have not listed in the solution. This should give the students the chance to be creative. Any correct answer should be accepted no matter how bizarre. We will be keen to hear what your class comes up with.
Problem
Brian, Margaret, Kim and Jo were looking at the objects below.
.gif)
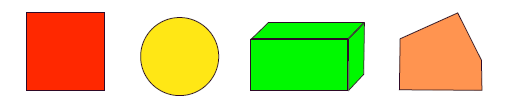
Brian says, Hey, the square is the odd one out.
Margaret says, No, Brian, the circle is the odd one out!
Kim says, No, it is the box!
Jo says, Well you are ALL wrong! The pentagon is clearly the odd one out.
Who is right and why?
Teaching sequence
- Show the students the four objects of the problem. Hold up the square.
Who knows what this is? What can you tell me about it? - Repeat step 1 for the other three objects.
- Here’s what the four friends Brian, Margaret, Kim and Jo said about these objects. Tell the students the problem.
- Get the students to tackle the problem in groups or on their own.
- As the students think about the problem, go round the class and write down some of their answers. Ask them if they can think of more than one way to separate the objects.
- Students who are able to do this relatively quickly could go on to the Extension problem.
- Get some of the students to report on what they have done. Suggest that a good way to gather all the information together is to write it in a table. Construct the table on a large piece of paper that can be put on the wall after the lesson ends. This table can be referred to later and even added to.
- Discuss the Extension problem.
Extension
Ask the students to find other objects in the classroom. Get them to say what makes them different from each other and from the four objects of the original problem.
Solution
In a way there is no solution to this problem because in a sense, each one of the students is correct. Brian is right because the square is red and the other objects are blue. Margaret is right because the circle is the only on that will roll. Kim is right because the box is the only 3-dimensional object. Jo is right because the other objects have symmetry (that is they can be rotated through quarter and half turns on to themselves) but the pentagon doesnt.
You might ask the class to find as many reasons as they can to explain why each object is really the odd man out. This information could be displayed in a table like the one below
|
square |
circle |
cube |
pentagon |
|
it's red |
it will roll |
it's 3-dimensional |
it has no symmetry |
|
it has four sides |
it has only one side |
it has 8 corners |
it has five sides |
|
it has four angles |
it has no angles |
it has 6 faces |
it has five angles |
|
it could be used to tile a floor |
? |
it has 12 edges |
it has exactly 2 right angles |
|
? |
it could be used as a dice |
? |
This table could be added to both in the different properties of the objects and in the types of objects. Hence the Extension could be incorporated into the table.
| Attachment | Size |
|---|---|
| Odd one out.pdf | 40.29 KB |
| Odd one out Maori.pdf | 50.42 KB |
Similar Resources
Odd Thing Out
List a number of properties that distinguish the 3-dimensional solids of the problem.
Devise and use Problem Solving Strategies to explore situations mathematically in particular guess and check, draw a picture, use equipment.
Mosaic Puzzles
Join shapes together to form other shapes
Identify and describe shapes
Devise and use problem solving strategies to explore situations mathematically (guess and check).
No Looking!
This is a level 3 link geometry activity from the Figure It Out series.
Precision Flying
This is a level 4 geometry strand activity from the Figure It Out series.
Getting Round to It
This is a Level 3 Geometry activity from the Figure It Out Series.
