Number Crunching

Problem One

A number line or hundreds board is a useful model for solving this problem. Numbers can be eliminated as the clues are considered.
I am between 50 and 75:

I am even:

When you add my digits, the answer is even:

I can be divided evenly by 5:

Other “What Number Am I?” problems can be solved in a similar way. For example:
“I am between 40 and 60. I am odd. My digits add to seven. What number am I?”

Problem Two

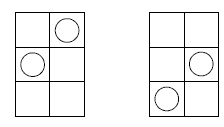
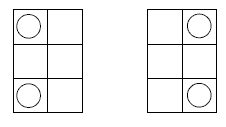
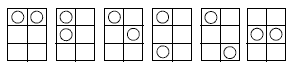
The initial assumptions the students make play a part in the number of possible arrangements. For example, the arrangements below may be considered the same because they can map onto each other by rotation:

Similarly, these arrangements may be considered the same because they map onto each other by reflection:

If these rotation and reflection assumptions are accepted, there are six possible arrangements (see the diagrams in the Answers section).
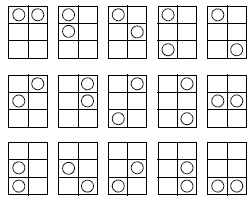
However, if the six positions are assumed to be individual, there are 15 possible solutions (see the diagrams in the Answers section).

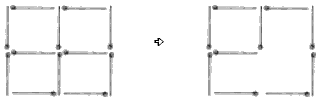
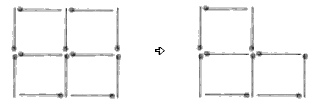
Problem Three

Students’ assumptions may prevent them from solving this problem, particularly if they believe that the squares must be the same size.

Students might like to solve this related problem:
Form three squares by removing two matchsticks.

They may wish to make up matchstick removal or addition puzzles for other students to attempt.

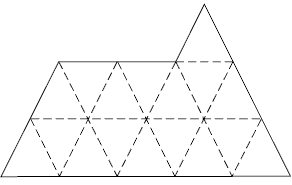
Problem Four

Encourage the students to visualise how the triangle would fit repeatedly into the shape and what lines would be created by meeting sides:

Students might use triangular pattern blocks to find other figures with an area of seventeen triangular units. Alternatively, they may want to draw their figures on isometric dot paper.

Answers to Problems

1. 60
2. If those that map onto each other by rotation or reflection are not included, these are the possible arrangements:

If rotation or reflection are included, these are the possible arrangements:

3. One possible solution:

4. a. 17
b. Answers will vary.