This problem solving activity has a logic and reasoning focus.
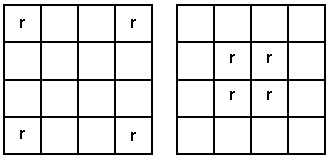
Miriama is building a large square window made up of 16 red and white panes.
What is the smallest number of red panes she can put into the window so that no three of them are in any row or column and so that she cannot put in another red pane without three being in the same row or column?
- Use symmetry and rotation to create geometric shapes that satisfy the no three in a line condition.
- Explore symmetric arrangements.
This problem requires students to use a systematic approach in order to be able to justify that all possibilities have been considered.
- find some answers to a problem;
- think about whether there are any more answers or not;
- try to explain why there are no more answers.
The problem also challenges students to recognise the symmetry in a figure, and to see that by rotating a figure through a quarter turn either clockwise or anticlockwise, two 'answers' are essentially the same. Symmetry through a line in the plane of the square is therefore important.
See also these Logic and Reasoning problems: Strawberry Milk, Level 1; Strawberry and Chocolate Milk, Level 1; Three-In-A-Line, Level 2; No Three-In-A-Line, Level 3; No-Three-In-A-Line Again, Level 5; and No-Three-In-A-Line Game, Level 6.
- Bottles tops
- Coloured pens and paper
- Copymaster of 4 by 4 windows
- Copymaster of 5 by 5 windows
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
The Problem
Miriama is building a large square window made up of 16 red and white panes.
What is the smallest number of red panes she can put into the window so that no three of them are in any row or column and so that she cannot put in another red pane without three being in the same row or column?
.gif)
Teaching Sequence
- Talk about square windows and their symmetry. Discuss approaches to any similar problems.
- Pose Miriama’s problem and discuss any difficult ideas.
- Have the class work on the problem in groups. A computer-made grid might assist in the task.
- Support the students as appropriate, encouraging them to use a systematic approach to get all possible answers and to record all their working.
- As solutions begin to emerge, share as a class.
- When they are ready, encourage students to attempt the extension problem.
- Choose groups that have used different approaches to the problem to report back and share their solutions and working.
- Discuss their conclusions.
- Allow time for students to revise and write up their solutions.
Extension
(a) Miriama now wants to put 25 panes in her red and white window.
What is the smallest number of red panes she can put into the window so that no three of them are in any row or column and so that she cannot put in any more red panes without three being in the same row or column?
(b) Miriama wants to make a square window made up of 16 red and white panes. What numbers of red panes can she put into the window so that no three of them are in any row or column and so that she cannot put in another red pane without three being in the same row or column?
Solution
In the same way as No-Three-In-A-Line Again, Level 5, we can show that three won’t work. However, 4 will and in two ways. This can be justified by working systematically. The two possible answers are shown below.