Purpose
The purpose of this activity is to support students using their knowledge of teen numbers to recall addition facts with nine.
Achievement Objectives
NA2-3: Know the basic addition and subtraction facts.
Required Resource Materials
- Counters (circular, square or novelty counters)
- Blank tens frames (use page 2 of Material Master 4-6)
- Masking card (A5 size is good)
Activity
- Set up models using the counters and frames to remind students of the place value structure of teen numbers. For example:
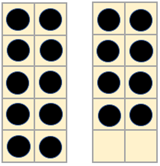
- Discuss the model: How many counters are here? How do you know?
Reinforce the linguistic connections. Eighteen is eight plus ten. Teen means a single ten.
Note that the way we say teen numbers (i.e. nine + teen) is in reverse order to their structure (i.e. 10 + 9) and is not consistent with the way we say other two-digit numbers, such as 43 which is said as forty-three but written s 40 + 3.
- Display a different teen number (e.g. 15 as 10 + 5) on the tens frames. Move one counter to create a nine plus example (e.g. 15 as 9 + 6).
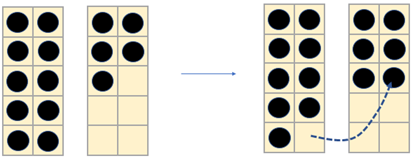
- Discuss the model: If 10 + 5 = 15 what is 9 + 6? How do you know? How can you use the counters and tens frames to explain these facts?
Students should realise that the total number of counters, 15, is conserved as one counter is moved from the left side to the right.
- Provide a masked example of a teen number to encourage students to image the process (e.g. 17 as 10 + 7). For example: I have made 17 under here. What does that look like?
Look for students to recognise the place value structure of the teen number (i.e. 10 + 7 = 17). Record this as an equation.
Keeping the frames masked, move one counter from the left side to the right side.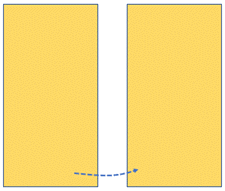
- Discuss the model: What addition fact have I made now? (9 + 8 = 17)
- Use the tens frames and counters to model 9 + facts. For example:
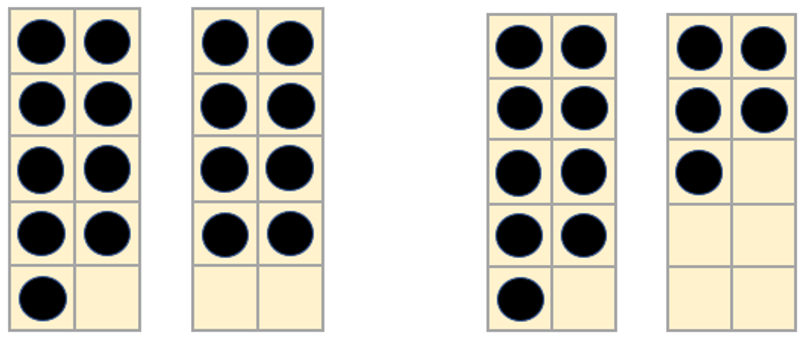
What is 9 + 8? What is 9 + 5?
- Discuss the models. Look for students to recognise that any nine plus model can be transformed into a ten plus model where the sum is a teen number.
- Build up a collection of nine plus facts. Record the results and display them as a vertical pattern of addition facts. Leave some spaces in the pattern or write the whole pattern and then rub out or conceal some of the expressions. For example:
9 + 3 = 12
9 + 5 = 14
9 + 6 = 15|
9 + 9 = 18
- Ask: What facts are missing?
Look for students to use patterns and derive their answers from the expressions still shown.
Erase an increasing amount of the shown facts and ask students to recall the missing expressions from memory.
What is 9 + 8? What is 9 + 4? What is 9 + 2? What is 9 + 7?
- Once the full pattern is recorded vertically ask students what patterns they notice. Look for generalisations. For example:
The sums are always teen numbers.
The sums have one in the teens place.
The sums have a ones digit that is one smaller than the number added to nine.
- Provide students with lots of opportunities to practise and learn the 9 + facts, and to express their mathematical thinking in different ways (e.g. online tasks, written, verbal, drawn diagrams, acting out, using physical manipulatives).
Next steps
Patterning supports students to connect the addition facts which aids memory. Use the strategy for remembering nine plus facts to support learning of the eight plus facts.
- For example, show the students 8 + 6 across 2 tens frames:
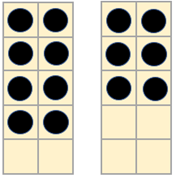
- Here is 8 + 6. How many counters do I move to make it ten plus something?
Look for students to recognise that 8 + 6 is equal to 10 + 4 = 14.
Continue using this method to learn the rest of the eight plus facts.
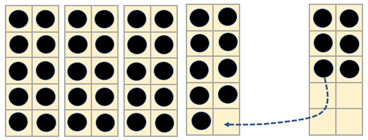
- Connect nine plus facts to other, more complex additions using place value. For example: Here is 39 + 6. If I move one counter, what can I make? What is 39 + 6?
Add to plan
Level Two