This is a level 4 activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (1219 KB)
Forming a conjecture involves looking for a pattern or rule, testing it, and then either using it for further exploration, modifying it, or rejecting it. Introducing students to the process of making conjectures helps them to learn how to think and communicate mathematically.
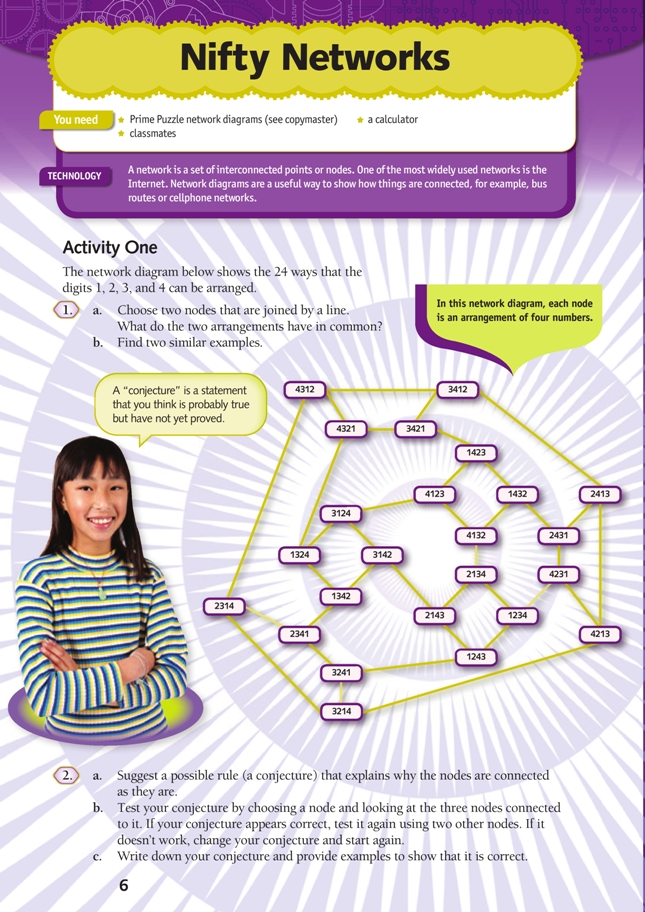
In this activity, students explore a network that links 24 arrangements of the digits 1–4. They are asked to form a conjecture about why particular arrangements are connected. Students also solve a network puzzle involving products of three primes.
a calculator
Prime Puzzle network diagrams (see copymaster)
FIO, Technology Transformations, Levels 3+-4+, Nifty Networks, pages 6 - 7
Network diagrams are a useful way to organise information. Unlike many other diagrams, the size and location of lines and shapes are irrelevant in network diagrams; all that matters is what is connected to what.
Activity One
Encourage students to use mathematical language as they explore the network diagram. For example, “My conjecture is that two numbers in the arrangement need to be different. At first I thought this was different from Sasha’s conjecture, which is that two numbers have to be the same. Then we realised that having two numbers different is the same as having two numbers the same. I tested my conjecture by checking three nodes on separate parts of the network diagram, and it worked for all of them. I didn’t check all 24 nodes because it didn’t seem necessary. If I wanted to prove my conjecture, I could check all the nodes, but I am confident that my conjecture is true.”
Most students will identify that connected arrangements have exactly two numbers in the same position. However, each arrangement is only connected to three nodes, when for each there are six possible arrangements with two numbers in the same place. For example, for 1234, these six arrangements can be made: 1243, 1432, 1324, 4231, 3214, and 2134. Exploring other nodes will confirm that the rule that determines which nodes are connected has a limiting component that excludes any arrangements where the numbers that remain unchanged are not the 1st and 2nd, 2nd and 3rd, or 3rd and 4th numbers.
The network in Activity One is based on a similar network created by the Isaac Newton Institute for Mathematical Sciences. See www.newton.ac.uk/wmy2kposters/june/index.html for further information about networks, including an explanation of how a network can be used to find an efficient pathway through a maze.
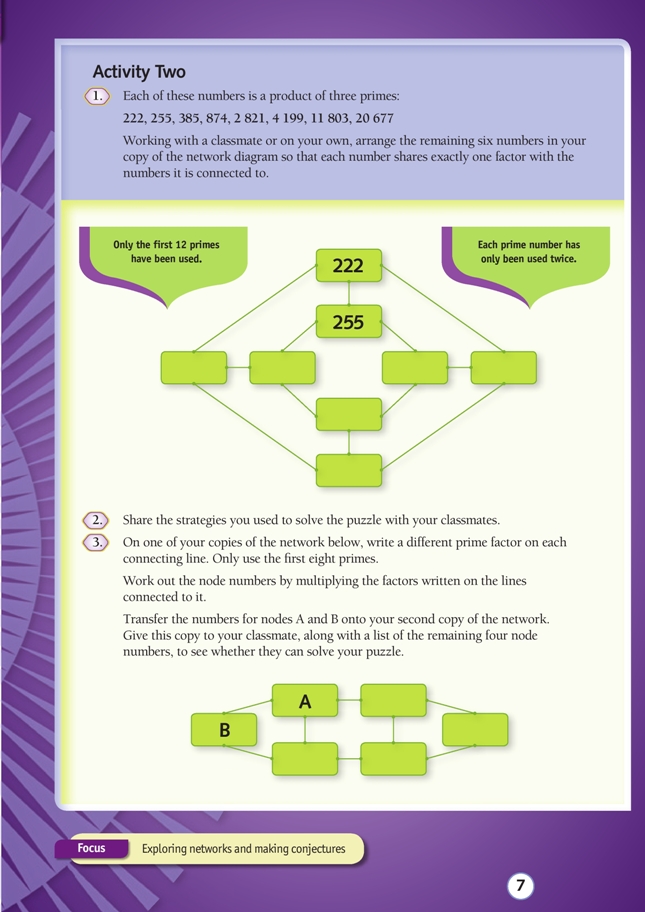
Activity Two
Problem solving is the core of mathematical thinking. By definition, a “problem” is something that may involve struggle. The process of grappling with a problem, returning to it after a break if necessary, develops persistence and resilience. Resist the temptation to simplify the network problem by guiding students through it. To do so is to rob students of the rewards of reaching a solution. And it does not help them develop problem-solving skills and dispositions.
Encourage students to look for possible strategies. Suggest that, even when using a strategy, it’s a good idea to work in pencil.
Once students reach a correct solution, tell them to return to the problem, asking themselves the following questions: What have I learned? Could I solve the problem again? Were any parts of my solution the result of luck? How could I use what I have learned to solve the problem more efficiently? Then ask students to share their strategies with their classmates.
An example of a strategy is outlined below:
First, list the first 12 primes (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37).
Next, find the 3 prime factors of each puzzle number. Some of these can be found using divisibility rules for 2, 3, 5, and 11 (see www.mathsisfun.com/divisibility-rules.html). Each factor has only been used twice; this information makes it easier to identify factors for the two largest numbers.
The prime factors of each number are:
222 – 2, 3, 37
255 – 3, 5, 17
385 – 5, 7, 11
874 – 2, 19, 23
2 821 – 7, 13, 31
4 199 – 13, 17, 19
11 803 – 11, 29, 37
20 677 – 23, 29, 31
There are 8 nodes and 12 lines in the diagram. Each pair of nodes is linked by a different common factor. Writing this factor beside each line helps to keep track of which factors have been used.
222 and 225 have been placed in the diagram. These two numbers have a common factor of 3. This leaves 2 and 37 for the lines joining the two adjacent nodes.
874 is the only other number with a factor of 2, and 11 803 is the only other number with a factor of 37, so these numbers can be added to the diagram:
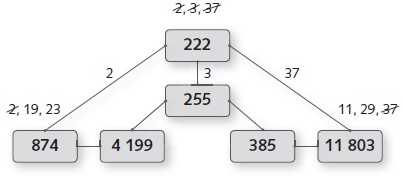
Next, find the number that is joined to both 255 and 874.
The factors of 255 are 3, 5, 17. The factors of 874 are 2, 19, 23. But some of these factors have already been used twice (2 and 3), so the “available” factors are 5, 17, 19, and 23. Looking at the list of factors, there is only one number with two of these primes as factors: 4 199.
It becomes increasingly easy to place the remaining numbers as the pool of available factors decreases. List the factors, cross out factors that have been used elsewhere, and identify which number combines two of the remaining factors (one from each side).
Students will enjoy learning how to create their own network puzzle for a classmate to solve. Encourage students to apply what they learned in question 2 to solve their classmate’s puzzle.
A related activity from the Figure It Out series is Safety in Numbers, found in the level 3+–4+ Technology in Practice book (pages 2–3).
Solving complex problems develops the key competency thinking.
The prime puzzle was adapted from a puzzle on the NRICH maths website (see http://nrich.maths.org/2414). The site provides further information about networks and several related activities.
Technology-related student activities
- Discuss information and communication technologies used in your home and at school. How would life be different if these technologies were not available?
- Use information and communication technologies to collaborate on a project with students at other schools (nationally and internationally).
Exploring the technology-related context
The Internet is an information network that links computers throughout the world. In technology education, ICT gives students the opportunity to design and plan outcomes, to present technological information to stakeholders, to research existing products and past designs, and to test models.
Answers
Activity One
1. a.–b. Answers will vary, depending on the pairs that are chosen. Possibilities include: the first two numbers are the same; the middle two numbers are different.
2. a.–c. Answers will vary. One conjecture may be that “arrangements that have two numbers in the same position are connected”. For example, 3241 is connected to 3214 (first two numbers the same), 1243 (middle two numbers the same), and 2341 (last two numbers the same). Having two numbers in the same position is the same as having two numbers different.
Activity Two
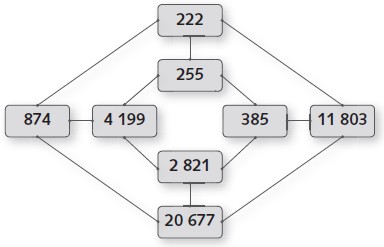
1. 
2. Discussions will vary.
3. Practical activity.