This problem solving activity has a number focus.
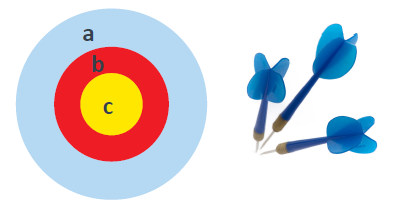
Afzal has three darts and this dartboard.
He is able to get each of the totals below, but no others, if every dart lands in one of the scoring regions on the board.
9, 11, 13, 15, 17, 19, 21
What values can a, b and c have?
Honor has 4 darts and this dartboard.
If she uses all of her darts she can get all of the totals below.

28 20 12 4
26 22 14 6
24 18 10
22 16 8
How are the regions on Honor’s dartboard numbered?
- Identify and describe patterns in numbers.
- Use expressions and words to describe number patterns.
- Work systematically to find the possible outcomes.
This problem gives students the opportunity to be systematic in the way that they combine numbers, be alert to number patterns, and to express patterns in simple expressions and with the use of their own language. The challenge is to see what scores can be made.
Similar Number problems include: Darts, Level 3, Super darts, Level 3 and Dartboards, Level 4. We suggest that you do Dartboards, Level 4 before you do this problem as this is an extension of that problem.
The Problem
Afzal has three darts and this dartboard.
He is able to get each of the totals below, but no others, if every dart lands in one of the scoring regions on the board.
9, 11, 13, 15, 17, 19, 21
What values can a, b and c have?
Honor has 4 darts and this dartboard.
If she uses all of her darts she can get all of the totals below.

| 28 | 20 | 12 | 4 |
| 26 | 22 | 14 | 6 |
| 24 | 18 | 10 | |
| 22 | 16 | 8 |
How are the regions on Honor’s dartboard numbered?
Teaching Sequence
- Draw the first dartboard on the board and pose the problem.
- If the students have completed Dartboards, Level 4 ask them to think about how this problem is similar. List ideas that were useful in solving Dartboards.
- As the students work on the problem ask them to explain the approach they are using.
How did you start this problem? Why?
What understandings are you using about number? How are you using them?
Can you see any patterns in the numbers?
Could you write an expression to show this pattern?
Are you working systematically? How? How could you be more systematic?
What do you still need to work out? - Share solutions for Afzal’s problem.
- Pose Honor’s problem for the students to work on.
- As they work, ask questions that focus on their manipulation of numbers using the number operations. Encourage them to justify their solutions.
How did you begin? Why did you start there?
How did you work out the numbers?
What information was the most useful? Did you need it all?
Are you convinced you have the solution? Might there be another one? Why or why not? - Share solutions.
Extension
What is the largest number of different totals you would expect for a 4 region dartboard with 4 darts that, when thrown, all hit the dartboard?
Can you generalise?
Solution
On Afzal’s board, if 3 darts ‘hit’ the same region then the total will be a multiple of 3. Since the only multiples of 3 among the totals are 9, 15 and 21, then the numbers on the board are 3, 5 and 7. These give the values of a, b and c.
On Honor’s board, if 4 darts hit the same region then the total will be a multiple of 4. Unfortunately there are a number of totals that are multiples of 4 here. However, we can get the biggest and smallest totals by getting all four darts in the regions with the biggest and smallest numbers, respectively. So the biggest number is 7 and the smallest is 1.
The next biggest number will be obtained by three darts in the 7 region and one in the next highest region. So 26 = 3 x 7 + the next highest number. So the next highest number is 5.
The next smallest total after 4 is found by having three darts in the 1 region and one in the next smallest region. So 6 = 3 x 1 + the next smallest number. So the next smallest number is 3.
So the regions are numbered: 1, 3, 5, 7.
Check that you can indeed get all of the totals using these four numbers.
Solution to the Extension
Suppose we have the four numbers a, b, c and d. Then let’s work out all possibilities carefully and systematically.
All four darts in one region: 4a, 4b, 4c, 4d. So there are 4 totals of this type.
Three darts in one region and one in another: 3a + b, 3a + c, 3a + d (that’s 3 and you get 3 more for each of 3b, 3c, 3d). So there are 4 x 3 = 12 totals of this type.
Two darts in one region and two in another region: 2a + 2b, 2a + 2c, 2a + 2d, 2b + 2c, 2b + 2d, 2c + 2d. So there are 6 totals of this type.
Two darts and one in each of two different regions: 2a + b + c, 2a + b + d, 2a + c + d (that’s 3 and you get 3 more for each of 2b, 2c, 2d). So there are 4 x 3 = 12 totals of this type.
All darts in different regions: a + b + c + d. There is 1 of this type.
Altogether then we have 4 + 12 + 6 + 12 + 1 = 35.
If you have n regions and n darts, why is the answer
[(2n - 1)(2n - 2) … (n + 1)] / [(n – 1)(n – 2) … 2 x 1]?