In this unit we look at ratio in the context of objects, physical space, geometric quantities and mixable things such as paint.
- Find relative numbers of objects, and the lengths of sides, with a given ratio.
- Find relevant fractions using given ratios.
- Find relevant rations using given fractions.
- Find ratios between three objects.
Ratios, proportion, and fractions are related concepts that are relevant to real life and mathematical situations. A ratio is a relationship between measures. For example, green paint might be mixed in a ratio of 1:3 meaning one measure of blue paint is combined with three measures of yellow paint. If the ratio is applied consistently then different quantities of paint can be made of the same colour. A four litre mixture will contain one litre of blue and three litres of yellow, whilst a 1 litre mixture will contain 250mL of blue and 750mL of yellow. The key information in this situation is that the ratio of 1:3 is upheld when one of the quantities represented in the ratio changes.
Ratio is a particularly valuable concept in the context of scale drawings. The ratio of the drawing to the actual object gives the idea of the relative size of the drawing to the object. Ratios and proportions are also fundamental to trigonometry, coordinate geometry and calculus.
The unit This is to That, Number, Level 4, gives an introduction to ratios, and relates them to proportion and fractions, and can therefore be used as a precursor to this unit.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- beginning with simple ratios, e.g., 1:2, 1:3, and 2:3, and using objects like connecting cubes to model the ratios
- using symbols for ratios and fractions alongside physical and diagrammatic models
- asking predictive questions to encourage students to think beyond what is visible, e.g., If you make three copies of this ratio, 2:3, what ratio do you have in total?
- developing students’ ability to find common factors when learning basic multiplication and division facts, e.g., Simplify the ratio 20:25
- allowing the use of calculators for predicting and confirming calculations
- progressing to working with the symbols alone, with the option of folding back to materials.
The contexts for this unit are mixing substances and using scaling to make models. This involves ideas like scale models, mixing fruit drinks, and making fertiliser for the garden. These contexts might be supplemented by, or adapted to, better reflect students' interests, cultural backgrounds, or to make connections to learning from other curriculum areas. Examples might include ratios in cooking, ratios of positions in sports teams or genders in a class, or in the dimensions of human faces.
Te reo Māori kupu such as ōwehenga (ratio), hautanga (fraction), whakarea (multiplication, multiply), and āwhata (scale) could be introduced in this unit and used throughout other mathematical learning.
- Copymasters One, Two, Three, Four, Five and Six
- Geometric instruments: ruler, compasses, protractor, a tape measure several metres long
- Counters, cubes, and other materials (and/or digital representations) for students to use when modelling ratios
- Scale models
- A4 Paper
- "Treasure" for students to hide (session 4 - students could provide this)
Session 1
In this session, students are introduced/reintroduced to ratios.
- Start with a whole class quick quiz about ratios in which students work in pairs or threes. If the concept of ratios is very new to your students, you might pose a smaller number of questions. At the end of each question, share students’ answers, model (and get students to model) the thinking involved, and decide collectively on the correct answer. Use the suggested questions below, adapted to a context that is relevant your class.
- I have twice as many eggs as you. You have 6 eggs. How many do I have?
- Jane has three times as many dogs as Bill. Bill has 4 dogs. How many dogs does Jane have?
- Bob has five times as many brazil nuts as Jenny. Jenny has four brazil nuts. How many brazil nuts does Bob have?
- I have twice as many eggs as you. I have 10 eggs. How many do you have?
- Jane has three times as many toy cars as Bill. Jane has 15 toy cars. How many cars does Bill have?
- Bob has five times as many strawberries as Jenny. Bob has 30 strawberries. How many strawberries does Jenny have?
- I have twice as many eggs as you. What is the ratio of the number of my eggs to the number of your eggs?
- Jane has three times as many toy cars as Bill. What is the ratio of the number of Jane’s toy cars to the number of Bill’s cars?
- Bob has five times as many strawberries as Jenny. What is the ratio of the number of Bob’s strawberries to the number of Jenny’s strawberries?
- If the ratio of my eggs to your eggs is 2:1, what fraction of our eggs do you have? What fraction do I have?
- If the ratio of Jane’s toy cars to Bill’s is 3:1, what fraction of their cars does Jane own? What fraction does Bill own?
- If the ratio of Bob’s strawberries to Jenny’s is 5:1, what fraction of the strawberries does Jenny have? What fraction does Bob have?
- Discuss the meaning of ratios like 2:3 and 1:5. For example, 2:3 means two units of one measure for every three units of the other measure. In ratios the units are the same. If the units are different that is called a rate, such as two windows painted for every three hours or two kilometres in three hours (snail’s pace).
- Break the class up into groups with no more than four in a group. Consider your students' prior knowledge of ratios, and organise these groups to include students with varying levels of mathematical knowledge and confidence to encourage peer learning, scaffolding, and extension. Give each group Copymaster 1. Ask students to make up their own 20 questions along the lines of the questions in 1 above. Ask students to record their own questions on the Copymaster, and their answers on the back, or on a Think Mat. During this time, you could also work with a small group of students to provide more scaffolded support
- Spend time sharing the problems and students' solutions as a class. Students from different groups could be paired up to share their favourite problems. Each group might share their favourite problem with the class.
Session 2
In this session, we consolidate ideas relating to ratio.
- Review the learning from the last session. Look for students to identify the meaning of a ratio as a relationship between measures and for them to justify their thinking with accurate examples. Address any misconceptions.
- Divide the session up into three parts and get the class to investigate the problems in Copymaster 2, Copymaster 3, and Copymaster 4 in each part. Students might work individually or in groups. Roam, provide support, and utilise the time available to work, in a targeted manner, with small groups and individuals.
Session 3
In this session students draw diagrams about ratios.
- Try to get hold of some scale models. Talk about the items and the way that ratio/scale is used for that object. Model cars or aeroplanes are a good example as the scale is usually displayed on the box. This box shows a scale of 1:43 which means a 1cm length on the model represents a 43cm length on the actual truck.
- Show students a metre ruler. Get different students to answer the following questions
How long would a stick be if the ratio of the ruler to the stick was 2:1; 5:1; 10:1; 1:2; 1:5; 1:10? For example, a 2:1 ratio would make the stick 50cm since every two centimetres on the ruler is represented by 1cm on the stick.
- Create a length of 25cm out of a long straw.
What is the length ratio of the metre ruler and the straw?
How might we figure that out?
- Emphasise that the straw fits into the ruler four times. This shows that four units on the ruler match with one unit on the straw. The ratio of ruler to straw is 4:1.
- Get students to work in pairs on Copymaster 5. The previous straw task will support students to understand what is required. Physical lengths made from 1 metre-long straws (available at dollar shops) will be helpful for some students. For example, compare strips that are 40cm and 100cm long.
How many times does 40cm fit into 100cm? (2 ½ times)
Each 10cm on the short straw is matched by how many centimetres on the metre straw? (25cm by finding quarters)
Is there a simpler way to record the ratio 10:25? (2:5 using a common factor of five)
- You might progress to using ratios to compare areas. Ratios are used in standard paper sizes such as A3, A4, and A5. Four A5 sheets fit into an A3 sheet so the ratio of area is 1:4. Area is a more complex attribute than length. Stay with rectangles and areas that map tidily into one another.
- Cut an A4 sheet in half, length-wise, to make an A5 sheet (coloured paper is good). Locate the A5 sheet in the corner of the A3 sheet.
What is the ratio of areas for these two sheets of paper?
Since the A5 sized sheet fits four times into the A3 sheet, the ratio of areas is 1:4 (meaning 1 cm2 of the A5 corresponds to 4cm of the A3 sheet.
- Ask students to create two rectangles in the area ratio of 1:2. That will mean the small sheet is half the area of the large sheet.
- Progress to 1:5 and then to 2:3 to see if students can transfer the ratio concept.
Session 4
In this session we draw a physical space to scale. This session provides an opportunity for the development of directional language, compass directions, coordinates on a plane, and procedural writing.
- Use maps with various scales. You might print off maps of parts of the local area using the Zoom function on Google Maps. Discuss the scale. Use questions, which reflect a relevant context, like:
I want to walk from the school gate to the town library. How far will it be? How long will it talk to walk that distance? How do you know?
I want to ride from Taupō to Wairakei. How far is that? How long will the ride take?
- Talk about drawing the school campus to scale (or use the classroom or some other physical space). Have a discussion with the whole class
What would be a useful scale to use?
How would you decide that? (size of paper; size of campus)
- Google maps will provide a very accurate bird’s eye view of the school. Use a printed map to create a treasure hunt. Each group needs a metre ruler, trundle wheel, or tape measure and some treasure to hide.
- Let the groups go outside and hide their treasure. They must use the measuring instruments to accurately mark the location of their treasure on the map. Locations should be some distance from buildings.
- When the groups return get them to exchange maps and try to find the treasure as marked on the map.
- After the treasure is found gather the class.
How is the scale on the map an example of a ratio?
How did you find the location of the treasure?
How was the scale useful?
Session 5
In this session students consider equivalent ratios in the context of mixing paint and other things.
- Pose this problem:
Henry mixes orange juice to water in a 1 litre jug in the ratio 3:1.
Reina mixes 9 litres of orange juice with 3 litres of water in a big container.
Which mixture will taste the most strongly of orange?
- Model the situation with orange and white cubes or draw a diagram. You might start with a model of Reina’s mixture, using each cube to represent 1 litre of liquid.

- Discuss the fractions in the mixture, 9/12 orange and 3/12 water.
Is there a simpler way to record these fractions?
Students might notice that 9/12 = ¾ and 3/12 = ¼.
Show how the fractions can be found by re-unitising the cubes into parts of 3 litres.
Try to show Henry’s mixture now. What does that look like?
- If students are consistent with the model, they will use one cube to represent 1 litre and sub-divide that cube into four parts to show 3:1
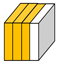
What fractions are in this ratio?
Students might notice the ¾ orange and ¼ water are also present.
What do the fractions tell us about taste?
You may need to mix different amounts of orange juice and water in the same ratio to convince students that taste is conserved if ratio is kept constant.
- Present similar problems, that reflect a relevant context, such as:
Koru mixes liquid seaweed to water in 5 litre container. He uses a ratio of 3:7.
Israel mixes 150 mL of liquid seaweed with 350mL of water to fertilise his tomato plants.
Which mixture will have the strongest smell of seaweed?
Model the problems using cubes or diagrams.
- Let students work on the problems in Copymaster 6. Use collaborative grouping so students can share ideas and benefit from tuakana-teina relationships (peer learning). Roam the room as students work. Look for:
- Do students know how to record ratios and explain their meaning?
- Do students recognise when ratios are the same, such as 1:3 and 100:300?
- Do students understand standard units of measurement and how those unit connect, e.g., 1000ml = 1L?
- Do students recognise that when ratios are not equal, that signifies a difference in a characteristic or attribute, like colour, taste or strength?
- Gather the class and discuss answers, highlighting the points above.
- Provide time for students to create a short presentation, utilising a presentation method that is relevant and engaging, that summarises their learning around ratios.
Dear families and whānau,
This week we have been solving problems involving ratios. Ask your child to explain how they would solve the following problems. Ask them to show you how diagrams help to illustrate a ratio problem.
- Jazmin has three times as many dogs as Anaru. Jazmin has 9 dogs. How many dogs does Anaru have?
- Michael has five times as many scorched almonds as Jenny. Michael has 55. How many almonds does Jenny have?
- I have twice as many eggs as you. What is the ratio of the number of my eggs to the number of your eggs?