In this unit the students will collect statistical data about their own class and school and learn how to compare it to data from students from CensusAtSchool.
- Plan a statistical investigation.
- Use technology to display and analyse data.
- Discuss features of data displays.
- Compare features of data distributions.
- Communicate findings.
By Level 4 students are able to take increasing responsibility for the planning and conducting of statistical investigations. Students should be capable now of incorporating technology into their work.
Informal measures of centre and spread (at curriculum level 4)
Formal measures of centre and spread are introduced at curriculum level 5. If your students are ready to explore these then look to curriculum level 5 activities. At curriculum level 4 we introduce the ideas of the middle and the middle 50% of numerical data. We can match the middle of the data on a graph up with the median in an informal sense using technology. We can identify the middle and the middle 50% using technology or marking by eye on a physical graph.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- varying the type of data collected; categorical data can be easier to manage than numerical data
- varying the type of analysis – and the support given to do the analysis
- setting up blank CODAP documents with the data already in and some graph blanks ready to use for students
- providing prompts for writing descriptive statements
- encouraging sharing and discussion of students' thinking
- using collaborative grouping so students can support each other and experience both tuakana and teina roles
- providing teacher support at all stages of the investigation.
The context for this unit can be adapted to suit the interests and experiences of your students. For example:
- the statistical enquiry process can be applied to many topics and selecting ones that are of interest to your students should always be a priority. For example, replace school uniforms with clothing for sports teams or cultural groups.
- Computers with internet access
- Various measuring equipment as defined in the planning
- Data collection cards
Session 1: Measuring the class
PROBLEM: Generating ideas for statistical investigation and developing investigative questions
- Tell the students that school uniform manufacturers may be interested in information about different body sizes. Introduce differences in sizes by asking for volunteers and standing two students up to discuss what about them could be measured to inform clothing or footwear producers.
Research online information about sizing guides as well. - Brainstorm things that could be measured and compared (height, head circumference, arm span, handspan, foot length). Ideas from this prompt should mostly be numerical (measured) variables.
Note: that some students may be sensitive about being measured. It is not appropriate to measure weight. Ideas around the ethics of data collection are attended to in 4. Students who do not want to be measured could become the measurer for a measurement station. - Ask what other things school uniform or sportswear manufacturers may be interested in to help with their creation of clothing or footwear. Brainstorm additional ideas to explore. Ideas from this prompt may tend to be more categorical variables.
- Once the initial brainstorming of ideas is done interrogate the ideas by checking them using the following questions:
- Is this a measurement/idea that the students in our class would be happy to share information with everyone? If not reject the idea [ethics].
- Can we collect data to answer an investigative question based on this measurement/idea? If not reject the idea [ability to gather data to answer the investigative question].
- Would you be able to collect the data to answer the investigative question in the timeframe we have (specify)? If not reject the idea [ability to gather data to answer the investigative question].
- What would be the purpose of asking about the measurement/idea that you have? If it is not purposeful then reject the idea [purposeful or interesting].
- Would the investigative question we pose involve everyone in the group (e.g. the class)? If not reject the idea [does not involve the whole group].
- Students to form small groups and select one attribute to measure (each group to select a different attribute). Ensure that one group selects height. Support the students to develop an appropriate investigative question to ask of the data. They should identify the variable of interest (e.g. height, arm length) and the group of interest (the class). Some groups might want to explore a categorical variable. This is ok as later they will have to do a measurement variable.
PLAN: Planning to collect data to answer our investigative question
- Discuss ways to collect and record the data considering that every group will have data they want to collect. Get students to develop a survey question with instructions to collect their measure (numerical and categorical).
- Exploring the guide on how to make measures for the CensusAtSchool questionnaire. The guide provides ideas on how to measure numerical data.
- See session 2 in Crunch the Coach and particularly the data collection stations for additional ideas.
- Measurement stations could be set up around the room for students to make their measures for the different survey questions designed. A recording card can be used to record individual student responses. See for example the data cards used in the 2019 CensusAtSchool survey. For categorical variables, the station will include the survey question with any response options.
- A suggested option for the class is to develop an online questionnaire where students can input their responses to all the groups different survey questions (from their individual data card), for example, using Google Forms. This reduces the amount of time needed to collate data and the data can be downloaded into a .csv file for analysis. It is good to think about any demographic data that would be useful as well, e.g. gender (be aware of sensitivity around this also). Names are not needed to be recorded, nor should any identifying demographic data be collected. The teacher needs to be aware of the overall survey and if there are any potential ethical issues. See more about ethics in How much bullying? activity.
Session 2: DATA: Collecting and organising data
- Students work around the different stations for the collective class survey questions and record the data onto their individual data cards. As the students gather data, the teacher should circulate and provide advice or assistance as required. Ensure that accuracy of measurements is maintained. Any students who were really not keen to be measured could be supervising a measurement station to ensure consistent and valid measures are made at it. For example, they could measure everyone’s height.
- Students to check in with one another about the measurements they have made. They are checking for errors in recording their results, errors in making measurements or errors in reading measurements. They should share and discuss their thinking.
- Once they have checked all their measurements and recorded results to any categorical survey questions get the students to input their responses into the class Google Form (or similar).
ANALYSIS introduction: Using an online tool to make data displays
In the remaining time for the session, the students will be introduced to using an online tool for data analysis. One suggested free online tool is CODAP. Feel free to use other tools you are familiar with. This is written with CODAP as the online tool and is assuming students have not used CODAP before. If your students are familiar with CODAP then they can move straight into analysing the data from the class survey.
If you do not want to use an online tool then head to the making displays part and progress with paper versions of bar graphs, dot plots and histograms.
Learning how to use CODAP
- Allow the students some time to get familiar with CODAP. Using the Getting started with CODAP example is a good starting point. This has a built-in video that shows the basic features of CODAP and gets you started using the tool. Other support videos can be found here.
- Note for teachers: Students will use the data collected in this session to make their displays in the next session. Between sessions download the survey data into a .csv file and set up the CODAP document with the data and share a link to this. See the video or written instructions on how to do this. Note the video and the instructions include getting started with CODAP too.
Session 3: ANALYSIS: Displaying and describing the data
Students use data from the previous session to produce graphs in CODAP or similar statistical analysis software.
- Discuss the data collected in the previous session and explain that the students will be using CODAP or similar software to produce graphs of the data to answer their investigative question(s).
- Share the link to the CODAP document that has all the class data.
- Students should first look at the data that is given and decide which variable(s) they need to graph to answer their investigative question.
- Initially students should be given freedom to experiment with what type of graph they feel best shows the information.
- Once groups have produced a graph or graphs to answer their investigative question, bring the class together and discuss the graphs produced. Most will have produced a dot plot (default graph for numerical and categorical data). CODAP allows us to look at this data in different ways.
Example of a categorical graph in CODAP: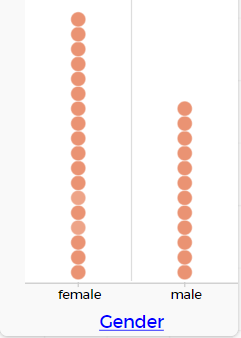
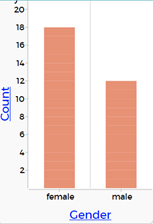
Example of a numerical graph in CODAP: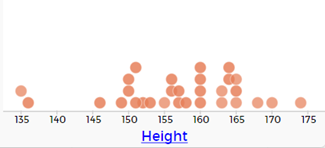
We might explore what is missing from the height graph (units) and show students how to include the units in the graph.
Click on the variable in the table or case card view. This gives a pop-up menu.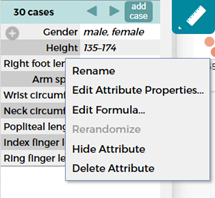
Select edit attribute properties, and in the pop-up window type in the unit (cm), and click apply.
This updates the graph to show the units.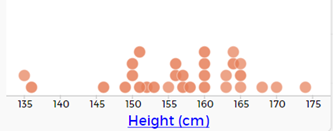
Students can update all the measurement variables in the table to include the units of measure. - Students will now learn about bar graphs (for categorical data) and histograms (for numerical data) as alternative displays.
- Making bar graphs in CODAP for categorical data: If they chose a numerical variable for their investigative question, get them to choose a categorical variable to practice this with. They should display the categorical variable they have chosen.
Click on the graph to bring up the tool bar. Select the graph icon and then select 'Fuse Dots into Bars' to make a bar graph.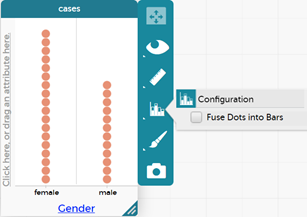
- Making histograms in CODAP for numerical data: If they chose a categorical variable for their investigative question, get them to choose the height to practice this with. They should make a display of the height first.
Click on the graph to bring up the tool bar. Select the graph icon and then select 'Group into Bins' (note the different option when numerical data is recognised).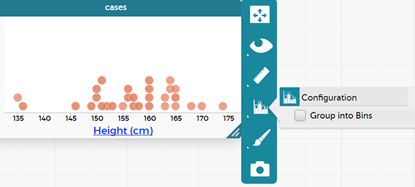
This action groups the dots into bins. Click on the graph icon again and now the options for 'Bin width', 'Alignment' and 'Fuse Dots into Bars' comes up. Generally, go with the default settings for bin width and alignment; then select 'Fuse Dots into Bars'.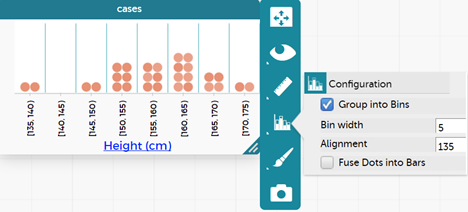
The resulting graph is: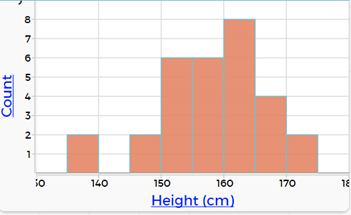
Students can explore changing the bin width and the alignment. What happens when the alignment is changed?
Students can compare the dot plot with the histogram and have a korero about what is similar and what is different. What are the advantages of the dot plot? What are the advantages of the histogram?
Remind them that they can use multiple displays to show different features of the data to answer their investigative questions. Students describe their data displays. A good starter is using “I notice…” as students start to notice features of their displays. For numerical data they might notice:
- The largest value
- The smallest value
- Where most of the values lie e.g. between X and Y
- Where the data peaks
- Gaps or clusters
- Unusual values
For categorical data they might notice:
- The most common
- The least common
- The majority
- Combinations of categories
- Any patterns (depending on the categories)
All statements in the descriptions need to include the name of the variable and the group, and for numerical data, the value and the units as well.
CONCLUSION: Answering the investigative question and reporting findings
- Students answer their investigative question using evidence from their analysis. Ensure students support each other and have opportunities to experience both tuakana and teina roles as they do this.
- Students can present their findings using a PowerPoint or similar presentation. Restrict to 3-4 slides
- Their investigative question
- Display(s) with descriptions (1-2)
- Answer to their investigative question – linking to the school uniform or sportswear manufacturer purpose
Session 4: Comparing to students like us in New Zealand
The class will use data from CensusAtSchool to compare to their class results.
- Students from around New Zealand have engaged in the CensusAtSchool questionnaire and measurement data has been collected, some like what we collected. This data is available on the CensusAtSchool site.
- In this session students will get their own sample of students their age from the CensusAtSchool database to compare with the class data from the previous sessions for measurement variables. The measurements you have taken will determine which variables you can compare. If students do not have an appropriate measurement variable get them to compare heights.
- Show students the CensusAtSchool random sampler, remembering to accept the conditions of use. Once in there familiarise the students with the tool. There are five parts to the tool.
- Select database – here we can choose any database from 2005 onwards. Recommend they use the 2015 or 2017 database as these have a larger range of body measurements.
- Select subpopulation – because we want to compare with other New Zealander students our age, we want to select specific years. When we select specific years, we get a drop-down list that allows us to select the same year level as the students. Select the year level. The example shows year 8 selected, but you could select any year group.
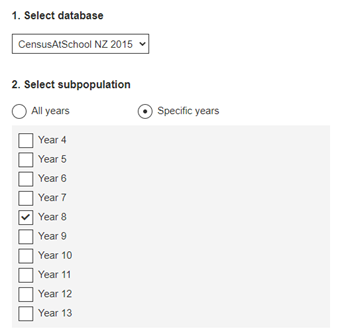
- Some students may want to also compare data by region. Ask if any students would like to share their iwi, hapū, marae, or location of other whānau connections with the class. They may decide to compare data from their home region with data from a region of Aotearoa they have iwi, hapū or whānau connections with.
- Select variables – because we want to look at measurements specifically, we only want to select specific variables. When we select specific variables, we get a drop-down list of all the variables in the survey. Suggest the following variables are selected:
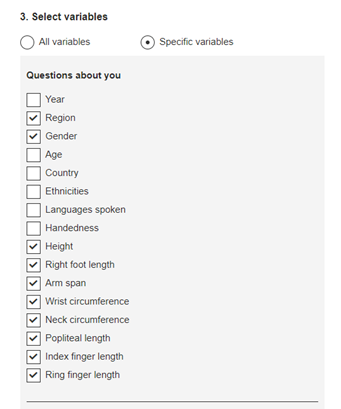
- Select sample type – leave as random sample
- Enter sample size (Maximum 1000) – suggest they select 100 to give a slightly bigger group to work with.
- Note: 100 is a good size for a later activity where we find the middle and the middle 50%, also 100 will give a bigger group (sample) size than the class and provides the opportunity to deal with comparing different size groups, something students sometimes think we cannot do.
- Once they have made the selections in the five parts, they click on generate sample and then download sample.
- Students save the .csv file and then import into CODAP. (The video here shows how to import data from CensusAtSchool.)
- Once the data has been collected from the site get the students to discuss how they might make a comparison with our class data e.g. they might suggest that a histogram is easier to compare than the dot plot.
- Students display the data for any variables we have identified that we can compare using CODAP. If they need to choose, suggest they choose height.
- They should write “I notice” statements about what they see in their data from CensusAtSchool.
- Focus the discussion on similarities and differences between the data sets, the class data and the CensusAtSchool sample (we are calling the group from CensusAtSchool, CensusAtSchool sample to describe the group. We are NOT doing sample to population inference – this is in curriculum level 5).
Note also that the different group sizes might be a sticking point for students as they may not think they are able to compare different sized groups. Get them to focus on the summary information e.g. where is most of the data, where does the data peak, what is the biggest value, the smallest value, the middle value, how do these compare? These were the suggested features from the description of their class data.
Note: If the students have all downloaded their own individual samples from CensusAtSchool the discussions each student makes could be quite different. If you want them all to have the same sample from CensusAtSchool you can download a sample yourself, import into CODAP and then share the CODAP document with your students (see this video on saving and sharing CODAP documents).
Session 5: ANALYSIS: Going deeper - investigating the middle and the middle 50% of our data using CODAP
Note that measures of centre are not introduced in The New Zealand Curriculum until level 5. At curriculum level 4 we introduce informal ideas of the middle and the middle 50%
Describing the middle
Students to work with their class data initially. The example given is for heights, but the ideas are the same for any numerical data.
Introducing the idea of the median, this is the middle of the data
- Make the graph for height using CODAP. Stretch the graph out so that the dots are not over top of one another. This can be done by dragging the bottom corner along so that the graph is wider.
- Select the ruler (measures) and tick 'Count' and add a movable value.
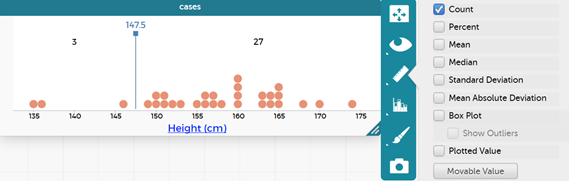
- Ask the students what they see on their graph now.
- They should see a line with a number in blue with a number on the top and two values, one to the left of the line and one to the right of the line. What do the two values (left and right of the line) represent? This is the count of the number of people in the class (in the given example it is 3+27, 30 students in the class).
- Discuss where the middle value would be, e.g. for this graph it would be in the middle of 30 which is 15, that is 15 on each side of the movable line.
- Therefore, we want to move the movable value so that the counts are about half each side.
- The place that we settle the movable value at is the middle value or the median. The median is the technical statistics term for the middle value in a set of data when the data are placed in order from smallest to largest.
- Get the students to read the middle value from their graph. In this example the middle value (OR middle height) is 157.5 cm (always include the unit).
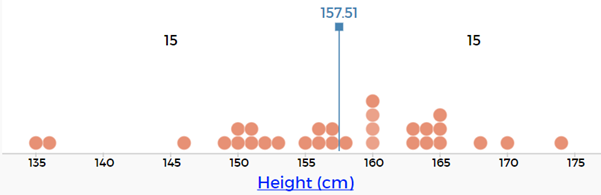
- They should now write a statement in a text box under their graph that says…
- The median height for students in our class is __________ cm.
Repeat the idea for the data they have from CensusAtSchool.
- Students make the graph for heights for the CensusAtSchool group.
- They click on the ruler and select 'Count' and 'Movable Value'.
- They move the line until they have about half on each side (if they have selected 100 students then there will be 50 on each side).
- They write a statement about the middle value of their graph.
- The median height for students in the CensusAtSchool sample is _________cm.
This special value, the median, can be found using the CODAP measures tool. Click on the ruler and then select median. They should get a red line showing the 'Median'. By hovering over this red line, they can find the median value, e.g. for first height example see picture below. They can also notice how close their guess at the middle was to the actual median (the middle of the values when placed in order from smallest to largest).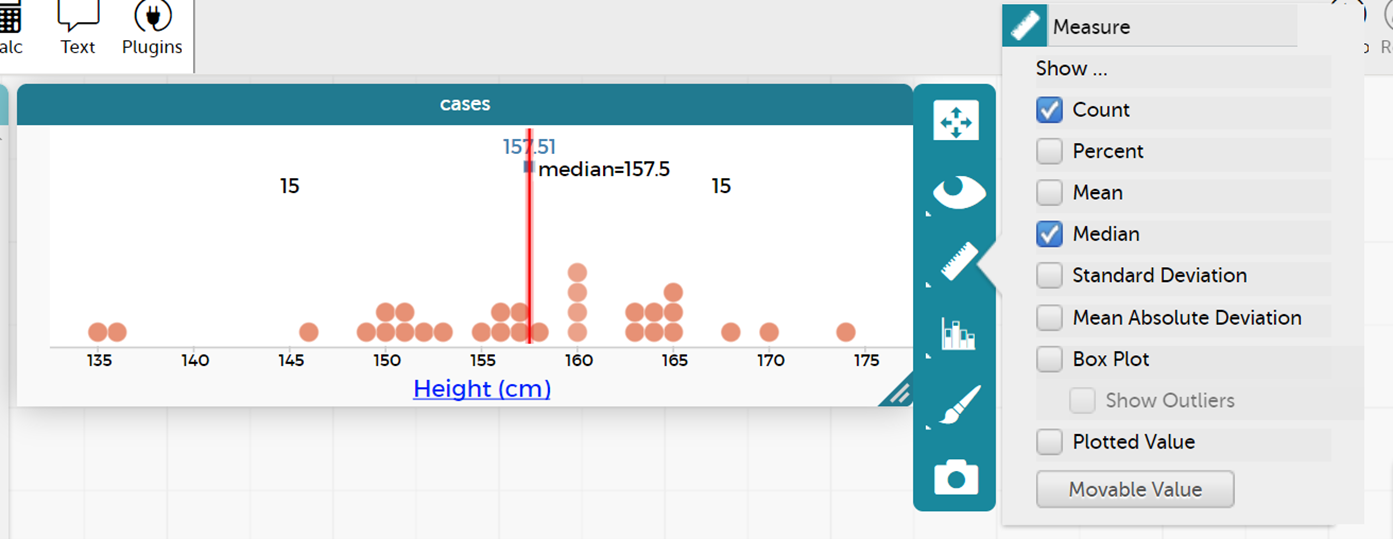
Introduce the idea of the middle 50% of the data
The “signal” for the data is often where the middle 50% of the data is.
- Go back to the class height graph
- Untick 'Median'
- Tick 'Movable Value' (add) so there are two movable values on the graph
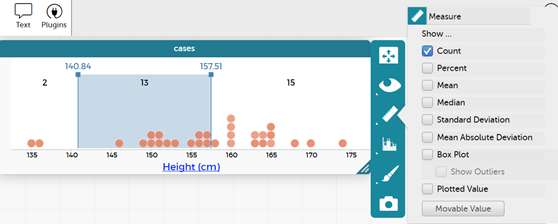
- Discuss with the students how many people would be in the middle 50% (in this case 15). This would leave 15 outside the middle 50% or 7/8 either side.
- Move the lines so that the counts match this or are very close to this.
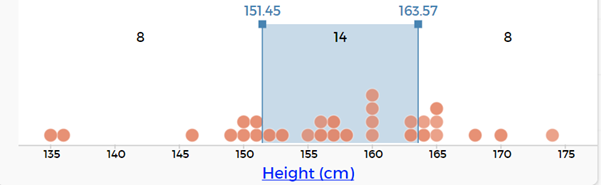
- Read the values for the middle 50%, from the two movable values. In this case it would be 151.5 cm for the bottom value and 163.5 cm for the top value.
- We would describe this as the middle 50% of heights for students in our class is between 151.5 cm and 163.5 cm.
Repeat idea for the CensusAtSchool sample heights data.
Making comparisons between our class data and the CensusAtSchool sample data
With these two additional pieces of information – the middle (median) and the middle 50% update your discussion around the similarities and differences between the class data and the CensusAtSchool sample data. Ensure students support each other and have opportunities to experience both tuakana and teina roles as they do this.
Dear parents and whānau,
At school this week we will be measuring the heights of the students in the class and comparing our results to the heights of students around Aotearoa. As another comparison we would like to be able to talk about the heights of family members. Could you please help your child measure the heights of their family members and record the information to bring to school?
Can each person in the family answer the following survey question:
How tall are you without your shoes on (answer to the nearest cm)?
Thank you.