In this unit we will explore the idea of having benchmarks of 1 litre and ½ litre or 500 millilitres, to aid in estimating the volume of given objects.
- Use objects of 1 litre volume/capacity to estimate the volume or capacity of other objects.
- Understand the need for standard measures of volume and capacity.
- Make sensible estimates about the volume and capacity of given objects.
- Carry out conversions between standard measures of volume and capacity (cubic centimetres, cm3, to cubic decimetres, dm3, and millilitres, mL to litres, L).
Volume is the measure of space taken up by a three-dimensional object. The space within a container is known as its capacity but as the thickness of many containers is negligible, it has become acceptable to refer to the space inside a container as volume too. In the measurement strand of the New Zealand Curriculum, volume and capacity are used as interchangeable terms (although the glossary describes capacity as the interior volume of an object).
Students need to develop personal measurement benchmarks. A benchmark is an understanding or a “feel” for the size of a measurement unit, which is useful when working with measures in daily life. Often these benchmarks are linked to familiar items such as a one litre milk bottle or a Pyrex jug.
This unit supports students to develop personal benchmarks for 1, 100 or 1000 cubic centimetres, 1 litre and ½ litre, and also strengthens students’ understandings of the relationship between litres and millilitres. Milli is the prefix for 1/1000 so 1 millilitre (1 mL) is 1/1000th of 1 litre and has a volume of 1 cm3.
The learning opportunities in this unit can be differentiated by altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- providing a smaller number of containers for students to work with, and ensure there are clear differences in the volumes of the containers provided
- providing opportunities for students to measure the volume of containers to confirm whether they hold more, less, or about the same as 1 litre after their initial estimates.
- providing opportunities for students to use fractional parts of 1 litre to describe volume, rather than millilitres e.g., one quarter of a litre rather than 250 ml.
This unit is focussed on measuring the volume of containers. Use a range of objects and containers that are familiar to your students to encourage engagement. Suitable examples are tissue boxes, cereal packets, Milo or biscuit tins, milk or fruit juice bottles, and toy buckets.
Te reo Māori vocabulary terms such as mehua (measure), rita (litre), kītanga (capacity), rōrahi (volume), whakatau tata (estimate), mita pūtoru (cubic metre), mitarau pūtoru (cubic centimetre) and ritamano (millilitre) could be introduced in this unit and used throughout other mathematical learning.
- Waterproof objects of a variety of volumes. Cardboard boxes can have a plastic bag inserted in them to hold water.
- Various bottles including several that hold 1 litre, e.g., milk bottle, fruit juice, shampoo.
- Place Value Blocks, including the large cube.
- Plastic bags (snaplock if possible)
- Measurement jugs
- Scrap cardboard, scissors, rulers and tape.
Session 1
For this session you will need plenty of bottles and containers of a range of sizes, including several that hold 1 litre. Fruit juice bottles, shampoo bottles, and yoghurt containers are particularly good containers for this task. You could either ask students to bring bottles and containers to school with them or collect them yourself. To ignite interest in this session, begin with a discussion around why it is important to know the amount that can be held in a container/ Possible contexts for framing this discussion could include looking at the ways in which people travelled to New Zealand (e.g. by ship, waka, plane etc.) or looking at planning the amount of food and drink needed for a school camp.
- Begin by selecting 5 or 6 containers of various sizes and shapes.
- Ask students which one they think has the least space in it. Introduce the word 'capacity' to mean the space within a container, and 'volume' as the amount of liquid or gas a container holds. Explain that although these terms mean different things, they are often used to talk about the same thing. It would be wise to choose one term to use with your class, throughout the sessions in this unit. Ask them to explain why they made their choice of container with the smallest capacity.
- Explain that we are going to order the containers from those that hold the least, to those that hold the most.
- Ask for suggestions for how to compare the size of the containers. Ensure that students understand that they are comparing the space inside the containers.
- Gather suggested strategies then trial strategies to establish an effective way to order the containers by volume. The most effective strategy will probably be to pour water from one container to another. If the water that fits in one container does not fit into another then the first must have been larger. Discuss how to organise the containers, given that only two can be compared at one time in that way.
- Group students and provide them several containers for each group. Ask each group to order their containers by capacity, from 'holds the least' to 'holds the most'. Watch to see that your students can organise the ordering of many containers, when the comparisons are two at a time. Consider grouping students together that have a range of mathematical abilities to encourage tuakana-teina (peer learning) and mahi tahi (collaboration)
- Share the techniques and strategies used by each group to order the containers.
- Ask 2 groups to pair up to combine their containers on one continuum of least to most volume. Check that they understand that volume is conserved (i.e. that it is the same quantity of water, even though its appearance may change in a different shaped bottle) and that the order of each group’s containers will not change by adding another group’s containers.
- Establish an order for all the containers available. This task raises efficiency and estimation. Suppose ten containers are already ordered by capacity.
What is the most efficient way to find the place of this (new) container amongst the others?
Students might suggest estimating first to get a ‘ballpark’ idea of where the new container might go. Next, compare the capacity of the new container to the others by pouring. How many pourings are needed? - An additional challenge can be to anticipate the water level if water is poured from a smaller container into a larger container. Rubber bands can be used to mark the predicted levels. Look for students to discuss strategies for anticipating the levels, such as considering the cross sectional area of the container.
Session 2
The following activities are to provide students with experiences to compare volumes/capacities of different objects and to create a benchmark for a container that holds one litre.
- Make a 1 litre container available for students to use to give them a ‘feel’ for one litre.
Compare it to a large Place Value Block cube.
Which object takes up the most space, that is, has the greatest volume?
The visual appearance of the large cube makes it look smaller than most other objects with the same volume of 1 litre (1000 cm3). It is fun to fill a bucket of water to the brim and ‘dunk’ the containers one at a time. The water that overflows is equivalent to the volume of the container or cube. - Group students and provide a variety of containers for each group. Ensure items that hold 1 litre (like a 1 litre measuring jug or a 1 litre container of milk or water) are included as such items will become useful benchmarks.
- Ask each group to draw and label the following buckets on large sheets of paper.
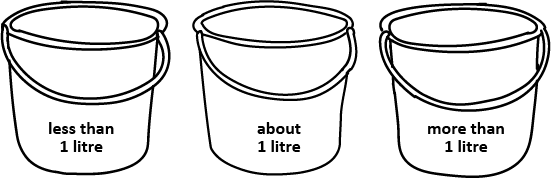
- Students work together to place the containers in the most appropriate bucket, then check their estimates using a 1 litre container. Be aware that interpretation of "lee than", "about", and "more than" is a bit subjective.
Gather the class and discuss the strategies students used to make their estimates. Consider the following points:
Do taller objects have more volume than shorter objects?
How does the cross-section affect the volume of the object?
If you have an object that you know is 1 litre, how do you compare its volume to that of an object that has different height and cross-section?
Provide students with this open challenge. They need scrap cardboard, scissors, rulers and strong tape.
Create a cuboid (rectangular prism), cone, or cylinder shaped container that can hold exactly 1 litre of water.
You may need to support students with creating nets, rolling pieces of card to form cones or cylinders, and applying their understanding of the fact that 1 litre equals 1000 cubic centimetres.
- Ask students to locate items from around their home that they believe would make good benchmarks for 1 litre and, if possible, bring them to school.
Session 3
In this session students compare their benchmarks for one litre and try to estimate one litre.
- Share the containers that have been brought to school as good benchmarks for 1 litre and identify which are closest to 1 litre in volume.
- Discuss which of the benchmarks are the most useful. For example, objects which you don’t usually see are not particularly good benchmarks as you will not be familiar with their volume. Common objects are easier to visualise.
- Give students a plastic bag and ask them to put one litre of water in it. Vary the size of the bags you use. You may prefer to do this activity outside.
- Compare the bags and discuss differences in appearance.
We know that all the bags hold 1 litre but they look different. Why is that?
Compare the bags to reliable benchmark objects. - Introduce millilitres as a unit that is helpful for measuring containers that hold less than a litre.
- What does milli stand for?
- How many millilitres equal 1 litre?
- How many millilitres equal 2.5 litres?
- How many litres equals 1500 millilitres?
You might use a small place value block to give students a sense of the size of 1 millilitre.
How many millilitres will fill a teaspoon? (5mL)
....a dessert spoon (10 mL)?
....a tablespoon (20 mL)?
Show the students a Place Value Block flat.
How many millilitres is this? (10 x 10 = 100)
How many lots of 100 millilitres make 1 litre? (10 since 10 x 100 = 1000)
Stack ten flats to form a large 1 litre cube to prove the result.
- Take several containers, measure the capacities, and express the measurements using both millilitres and litres, e.g. 750ml = 0.75 L. Discuss why 750 mL is the same as 750/1000 of 1 litres and is written as 0.75
Provide the students with some conversion examples between millilitre and litre measures, such as:
Millilitres Litres 500 mL 1 L 250 mL 750 mL 300 mL 0.3 L 900 mL 1200 mL 456 mL 0.456 L 685 mL 903 mL 0.728 L
Session 4
In this session students work with volume as the amount of space that an object takes up.
- Provide a range of familiar objects of different volumes (preferably things that will sink in water). Make sure all items are waterproof. Bath toys make good objects.
- Ask students which of the objects has the largest volume. If there is confusion, explain that volume does not just mean the amount that a container can hold, it also means the amount of space an object takes up.
- Show students how they can find the volume by displacement. Place a container full of water inside an empty container or tray. Submerge the object in the container of water and measure how much water is displaced (overflows) into the empty container. This is equal to the volume of the object – discuss why this is so with the class. If you can find a copy, read ‘Mr. Archimedes' Bath ’ by Pamela Allen.
- Allow students some time to experiment with this concept and to order objects by volume. Discuss the importance of considering all three dimensions, not just one dimension such as height.
- If you have plasticine available pose open challenges like:
Make a blob that has a volume of 48 cm3 which is the same volume as 48 mL.
Change the volume to provide more challenge, e.g. 0.124 L.
Session 5
- Bring this unit to a conclusion by asking students to share the benchmarks they are going to use for 1 litre.
- List the various benchmarks on a large sheet of paper to be displayed as a reference.
- Share the various strategies and techniques students have developed to establish near estimates for objects they are asked to estimate the volume of.
- Ask students to think about other possible accessible items that could be used as benchmarks to measure items that are less than 1 litre in volume.
What is the volume of a can of soft drink?
Why might that volume be a good ‘size’?
What is the volume of your lunchbox?
Why might that volume be a good ‘size’?
What would be a good volume for a chilly bin? - School bags and backpacks are often measured in litres to indicate the capacity of the bag. Research standard backpack sizes online to find out the usual dimensions.
Why is the capacity of a backpack important?
How many litres is your backpack in capacity?
Use the large Place Value Block cube as the benchmark of 1 litre to estimate the students' backpacks.
Dear family and whānau,
At the start of this week we would like each child to bring a plastic container or empty bottle to school. We are collecting containers of as many different sizes and shapes as we can. During the week, draw your child's attention to the labels of containers around your home and ask them to tell you the capacity of the containers in litres or millilitres.
If possible, do some baking with your child. Recipes usually include standard measures of weight and volume, such as grams (g) and millilitres (mL).