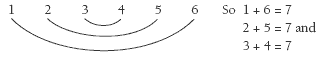This is a level 2 number activity from the Figure It Out series. It relates to Stage 5 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (161 KB)
use addition facts to solve addition problems
Number Framework Links
Use this activity to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in the domain of addition and subtraction
• give the students practice in recalling basic facts.
A pack of playing cards or 4 sets of 1-6 digit cards
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book Two, Make 28, pages 14-15
Two copies of record sheet Copymaster
A classmate
This is another version of the traditional nim game and will help students practise addition and subtraction facts. More importantly, it also provides a context for using logical reasoning and number patterns to devise a winning strategy.
Before using this as an independent activity, explain the rules and have the students play the game in guided teaching groups. Make sure that the students understand the game and the recording sheet. The whole class could play the game if you have enough decks of cards.
An alternative to using cards would be to have each student write the numbers 1 to 6 out twice and cross off the numbers as they use them.
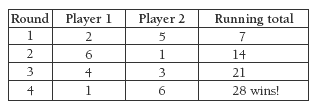
Make sure that the students play a number of games before discussing some winning strategies. Have them test the theories they come up with by playing the game. Resist the urge to tell them the winning strategy as long as possible so that it becomes the major goal of playing the game. When the winning strategy is becoming well known in the class, challenge the students to explain why the player who goes second should always add the number that makes a multiple of 7 to the number played by the first player. A table may make the pattern clearer.
It may be necessary to list the card numbers in order to show the 7s pattern:
The largest card number is 6, so the key numbers that control hitting 28 for the player who goes second are 21, 14, and 7. These are all multiples of 7.
Extension
Extend the digit cards to include 7 and make the winning target number 32 or 40. Another variation of the game would be to make the first person to reach the target number or higher be the loser. Challenge the students to work out a strategy rather than just playing the game.
Answers to Activity
1. Practical activity
2. a. Strategies may vary, but the best winning strategy is to aim for multiples of 7. Each time your classmate plays a number, play a card that makes a total of 7 or a multiple of 7. Your aim is to get to 21 (which is at least 1 short of your classmate being able to make 28 with their highest available card). They must then play a card to which you can play the last card to total 28. (If you are the first player, you will have to wait until your second turn to make a multiple of 7.)
b. It does not make any difference what the starting number is as long as you can make a multiple of 7 as soon as you can.
c. If you play second and keep to your strategy, you will always win. If you play first and can make a multiple of 7 on your second turn, then you will also win. But if both
players try to use the “multiples of 7” strategy, the player who goes second will always win.