Looking Ahead

Problem One

The students should be used to using a calculator to convert fractions to decimals. The illustration in the students’ book shows what a calculator display would show when 1 is divided by 3. It clearly shows that this is a recurring decimal.
When students divide 1 by 7, the standard calculator display will show 0.1428571. This could be a recurring decimal with the string 142857 recurring infinitely, but it’s impossible to know for sure without finding a calculator that displays more than eight digits or by doing long division. If students use long division to check, they should quickly see that 1/7 does convert to a recurring decimal.
To show that 142857 recurs, use the notation 0.142857, where the dots over the 1 and the 7 show that the section between and including these numbers repeats over and over again.
That string will in fact repeat eight times in the first 50 decimal places because 6 x 8 = 48. There will be two places still left after the eight lots of 142857. So the next two numbers will be 1 and 4.  This means that the 50th decimal place is occupied by 4.

Problem Two

Most students will find the solution to the problem outlined below easier to understand if they have worked with cubes first.
Wiha can’t carry enough food and water to walk straight across the desert, so she will have to leave a stash somewhere on the way. Use one cube to represent 1 day’s food and water.
To survive walking the last 80 kilometres, Wiha must have four bags at the 20 kilometre mark (or the mark that was 80 kilometres from the end). How does she get the four bags there?

She can get three bags there by starting off with four bags, but that isn’t enough to get her all the way across the desert, so she has to go back to get some more. She needs another bag to get back to her starting point, so she can leave only two bags hidden at the 20 kilometre mark on that first foray. It will take her 2 days to return to her hidden bags: 1 day to get there and 1 day to get back. If she starts at the beginning of the desert again with four bags, she will have three bags when she gets to the 20 kilometre mark, where she has stashed two bags. That means she has five bags
altogether. But she only needs four bags to get across the rest of the remaining 80 kilometres of desert and she can carry only four bags at a time, so she has one bag more than she needs. Therefore it would be sensible for her to take only three bags on her second “first 20 kilometre” trip:
one to use on the way and two to add to the store at the 20 kilometre point.
She now has four bags at the 20 kilometre mark and can use one of these during each of the next four 20 kilometre walks. So Wiha can get across in 7 days: 3 days to get four bags to the 20 kilometre mark and 4 days more to go the final 80 kilometres.
This process is shown as a diagram in the Answers.
Extension
You could vary the conditions. Perhaps Wiha has a companion who can only carry three bags. How long will it take the two of them to cross the desert?

Problem Three

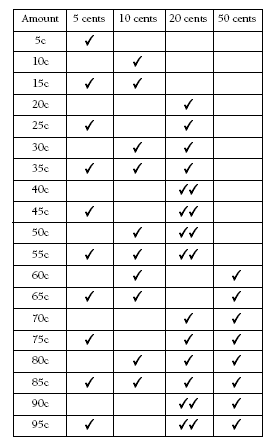
The students can use a table to find ways to make all the amounts from 5 cents to $1.05. Theyshould always look for the minimum number of coins needed to make each amount. Consider the amounts from 5 cents to 95 cents:

They can make all these amounts with a minimum of five coins: one 5 cent coin, one 10 cent coin, two 20 cent coins, and one 50 cent coins. The students might now see that they can make the final two amounts ($1 and $1.05) with the five coins that they have already used. And these five coins add up to $1.05, so they will use all the coins when they buy something for $1.05. So this is the correct answer.
If the students continued the table to find the minimum number of coins needed for $1 and $1.05, they would use two 50 cent coins. Added to the coins used previously, this would bring the minimum number of coins up to six, and it would also mean that they won’t use all the coins when they buy something for $1.05. Obviously, this can’t be the correct answer.

Problem Four

The students will have already encountered the relationship between the number of sides of polygons and the number of diagonals in Problem Three, page 7, in Problem Solving, Figure It Out, Level 3. This problem, which uses more sophisticated reasoning, should extend their understanding.
The students could count the number of diagonals in a hexagon. But it is more efficient to notice that there are three diagonals from every corner of the hexagon. So 3 x 6 = 18. But this counts each diagonal twice. So the answer is 9. Similarly, the students could draw and count for question b.
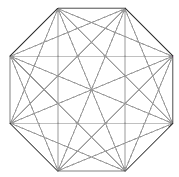
They will see that there are five diagonals from every corner of the octagon, and 5 x 8 = 40. But once again, this counts each diagonal twice. So the number of diagonals is 40 ÷ 2 = 20.
This can be used to find the number of diagonals for any polygon. The rule is (1/2 x the number of sides) x (the number of sides – 3). The number of sides in a polygon is the same as the number of vertices. The number of sides minus 3 equals the number of diagonals from each vertex. Why subtract 3? If you join a vertex of a polygon to every other vertex, you use the number of sides minus 1. In this question, you have to count only the diagonals. There is no diagonal from a vertex to the two adjacent vertices, so another 2 is subtracted. Altogether, 3 is subtracted.
To write this algebraically, with n being the number of sides or vertices, the formula is:
diagonals = 1/2 n x (n – 3).
Most students at this level won’t be ready for this algebraic notation, but more able students may be comfortable using it.

Hints for Students

1. What does 1/7 look like as a decimal? Try a smaller case than the 50th place.
Can you see a pattern?
2. You could try working backwards, use equipment, or perhaps use trial and
improvement.
3. Use equipment such as play money. Then use trial and improvement and record your results on a table. Remember that you are looking for the minimum number of coins.
4. Experiment with small cases first, for example, a square. Then look for a pattern.

Answers to Problems

1. 4
2. 7 days. You could show this in a diagram:

3. Five coins: 5c, 10c, 20c, 20c, and 50c
4. a. 9
b. 20

c. A possible rule is: Half the number of sides multiplied by three less than the number of sides. This can also be written as: 1/2 x (number of sides) x (number of sides – 3).