This unit examines the use of reflective, rotational, and translational symmetry in the design of logos. Logos are designs associated with a particular trade name or company and usually involve symmetry to make them aesthetically pleasing as well as functional.
- Find all the lines of reflection symmetry in a given shape.
- Identify the order of rotational symmetry of a given shape (how many times it "maps" onto itself in a full turn).
- Create designs which have reflection symmetry, rotational symmetry (orders 2, 3, 4, 6) and translational symmetry.
This unit centres on symmetry, particularly reflective and rotational symmetry, although there is some reference to translation symmetry. A shape has symmetry if it has spatial pattern, meaning it maps onto itself either by reflection about a line, or rotation about a point.
Consider the Mitsubishi logo. There are three lines where a mirror could be placed and the whole figure could be seen, with the image in the mirror forming the hidden half.
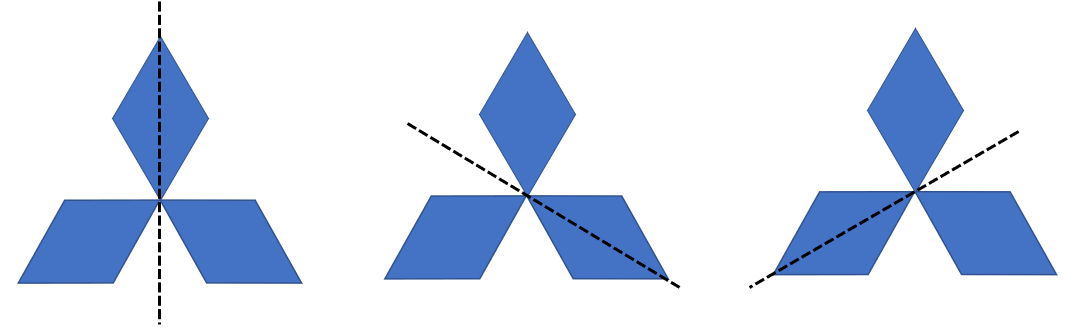
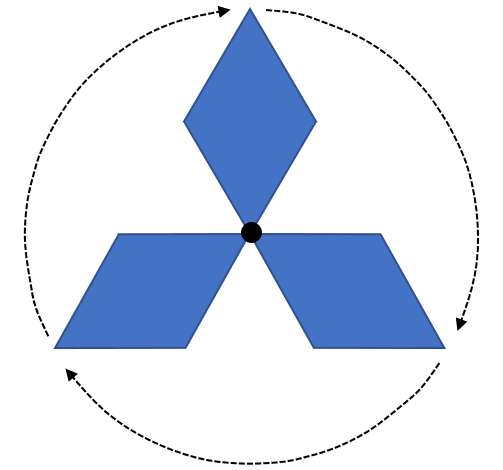
This logo also has rotational symmetry about a point. Each turn of 120⁰ (one third of one full rotation) maps the logo onto itself. Since the logo maps onto itself three times in a full turn of 360⁰, the figure has rotational symmetry of order three.
The mathematics of symmetry is found in decorative design, like kowhaiwhai in wharenui, and wallpaper patterns, and motifs such as logos. Human beings are naturally appreciative of symmetry, possibly because it is prevalent in the natural world. Creatures are approximately symmetrical and reflections in water are a common example of mirror symmetry.
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to support students include:
- ensuring that students have access to physical manipulatives that enable them to act out folds/reflections and turns of shapes
- modelling reflections and rotations, and expecting students to copy your actions before attempting problems independently
- helping students to represent reflections and rotations diagrammatically to ease memory load and support thinking, e.g. drawing lines of symmetry on a paper copy of a shape
- encouraging sharing and discussion of students’ thinking
- using collaborative grouping so students can support each other and experience both tuakana and teina roles
- encouraging mahi tahi (collaboration) among students.
Tasks can be varied in many ways including:
- beginning with simple shapes with limited symmetry and progressing to more complex shapes. In general, reflection symmetry is easier to see than rotational symmetry
- reducing the demands for a product, e.g. diagrams with less reliance on writing sentences
- using digital technology, such as PowerPoint and drawing tools, to create symmetrical designs using a beginning element.
The contexts for this unit can be adapted to suit the interests, experiences, and cultural backgrounds of your students. Capitalise on the interests of your students. Symmetry is common across all cultures of the world. Kowhaiwhai patterns on the rafters of wharenui (meeting houses), designs on Rarotongan tivaevae, Fijian tapa or Samoan siapo cloth usually involve symmetries. Look for examples of symmetrical design in the local community. Encourage students to capture symmetric patterns they see and use the internet as a tool for finding images in Aotearoa. Search for symmetry to show how common geometric patterns are throughout the world.
Te reo Māori vocabulary terms such as hangarite (symmetry, symmetrical), hangarite hurihanga (rotational symmetry), whakaata (reflect, reflection), huri (rotate, rotation), and neke (translate, translation) could be introduced in this unit and used throughout other mathematical learning.
- Design equipment (rulers, compasses, protractors, set squares)
- Circular lids
- Mirrors
- Scissors
- Paper circles (easily cut out of newsprint in batches by stapling the centre of a traced circle)
- Copymaster 1
- PowerPoint 1
- Connected 2, 1999, Samoan Siapo Pattern
Getting Started
- Fold a circle in half and cut pieces out of it in any way you like. Ask the students to anticipate the pattern that the opened-up shape might have. Write down any mathematical vocabulary that might arise, in particular, terms like symmetry, or reflection. Open the cut circle to confirm the students’ predictions. The shape has reflective or line symmetry along the fold line.

What pattern can you see in the shape?
How did the way we made the shape affect the symmetry it has?
You may want to show how the whole shape is visible if the mirror is located along the fold line.
Mirror symmetry and fold symmetry have the same meaning with 2-dimensional shapes. - Ask: Why is reflective symmetry sometimes called mirror symmetry, fold symmetry, and flip symmetry?
It is important for students to see that one half of the shape maps onto the other half by folding and flipping actions. Each alternative term can be demonstrated. Holding a mirror along the fold line enables students to see an image of the whole shape even when one half is masked. Similarly, the amended (cut) circle can be refolded in half and traced around. Then flip the paper over the fold line and trace around it again. The traced figure will be that of the whole amended circle. - Ask students to make their own shape by folding a circle in half and cutting out pieces (they must not cut all the way along the fold line). This will enable them to conjecture that all such shapes have at least one line of reflective symmetry (some may have two depending on the cuts). The symmetric shapes may be displayed on a chart.
- Move onto folding a circle into quarters (in half then in half again) and cutting pieces out.

Before opening up the circle ask:
What pattern do you expect the shape to have? - Confirm that the two fold lines are lines of reflective symmetry.
Is there another type of pattern in this shape?
Students may not recognise that the cutout shape has rotational symmetry as well. Trace around the shape on a whiteboard. Turn the shape one half turn (180⁰) to show that the shape maps onto itself.
The shape has half turn symmetry. How many times will it map onto itself in a full turn?
Students should predict order 2 rotational symmetry. That means the shape maps onto itself twice, in a full turn. - Ask students to create their own pattern using quarter folds of a circle. Ask them to compare their shape with that of a partner.
How are the shapes the same? How are they different?
Do both shapes have the same symmetry?
Most students will realise that there are two lines of reflective symmetry (the fold lines) but the half turn rotational symmetry is harder to spot. - Ask your students to anticipate then investigate what symmetry the circle shape will have if folded in eighths or sixths before cutting. Sixths can be created by folding the circle in half and then looping the half into thirds (see diagram below). (The circle folded into eighths will have at least four lines of reflection symmetry and rotational symmetry of order 4; with sixths the symmetry is six lines and order 3). Ask the students if they can see a pattern in the "least number" of lines and orders.
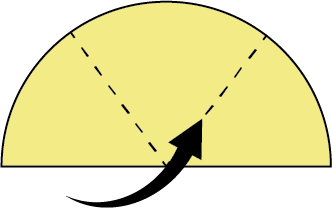
- Challenge the students to use paper circles to create a shape that has rotational symmetry of order 3 but no lines of reflective symmetry. Next ask them to produce a shape that has rotational symmetry of order 4 but with no lines of reflective symmetry. Then ask for a shape that has rotational symmetry of order 5 with no lines of reflective symmetry, etc.
Session Two: Car logos
- Begin by showing a short film clip of a car from a popular brand.
What make of car was that?
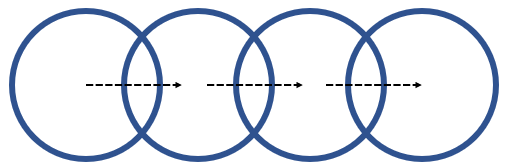
How do you know? - Investigate the logos found on motor vehicles by looking at cars in the school car park, magazine advertisements or images from the internet. PowerPoint 1 provides some common car logos. Car advertisements in magazines can also be cut out and used. Most manufacturers use symmetry of some kind in designing their logos. For example, Audi uses four intersecting circles in a line. This pattern has one line of reflection symmetry. This logo is created by translating (shifting) one circle three times.
- Discuss the symmetry of each logo and compile a list of car manufacturing companies for future reference. (You may need to omit the manufacturer’s name from some of the logos to get any symmetry. For instance, removing ‘Ford’ from its logo gives an elliptical shape that has two lines of symmetry.) It is just as important to identify logos that are non-examples of symmetry. For example, the logos for Volvo and Jaguar, and Peugeot have no symmetry, even when the company name is removed.



- Provide the students with drawing instruments such as rulers, protractors, drawing compasses, or jar lids, and tell them to recreate the car logos they saw in the car park, online or in magazines. Have the images available for them to refer to, if needed. At times it may be necessary to bring the class together to discuss construction skills. For example, for a logo involving rotational symmetry of order 3, a protractor will be useful. Since there are 360° in a full turn, one third of that is 120°, which gives the angle measured at the centre for dividing a circle in thirds. Construction skills like drawing a right angle by using a protractor or compass construction may be modelled if necessary.
Session Three: Logos in the media
- As homework (see Homelink) ask the students to find other examples of logos. Obviously not all logos have symmetry. Sporting goods manufacturers are good examples of this. Nike uses a “swish” that was designed to embody movement. Adidas uses three stripes etc. Examples will illustrate to the students that logos have to be both aesthetically pleasing (i.e. often symmetric) and suggestive of the nature of the company. Share the logos students bring along and group them by symmetry discussing what message is suggested by the logo image. This has strong links to visual language in the English curriculum. For example, the Canterbury Clothing Company has a logo of three translating, overlapping C’s with a kiwi inside them that give the impression of a single ball moving from left to right.

- Set up a matrix for classifying the logos. Create a chart by pasting logos in the appropriate cell. The Canterbury logo belongs in the bottom right cell as it has no reflective or rotational symmetry. It does have translation symmetry.
The Starbucks logo belongs in the bottom left cell as it has reflective symmetry but no rotational symmetry.

- Set up the following scenario for the students:
You work for an advertising company as a logo designer. There are five new companies that need new logos. They have stipulated that the logo must have some symmetry but must also suggest what goods and services they provide. (If you wish, they may also be required to come up with a slogan that captures the message, e.g. "Just do it".)
Here are the companies:- Sweeties - a company that makes sugar-free lollies that taste great and don’t ruin people’s teeth.
- Gadgets - who make neat construction gadgets (gears, blocks, wheels, etc.), so people can create their own toys.
- Mana - an after-school club that supports students in learning te reo Māori.
- Duds - makers of cool clothes especially for primary school children.
- Hapori māra - a community organisation that specialises in planting native trees
- Brainbuilders - the people who provide one-on-one tutoring service for students. You get one-on-one help so you are in a class of your own!
- Give the students sufficient time to design logos for one or more of the companies. They will need to present the logo in a short report to each company that shows what symmetries are involved and how the design suggests the goods or services the company provides. You may decide to set up a voting system for the class to decide on a winning logo for each company.
Session Four
- Provide your students with paper copies of logos (Copymaster 1). Display the logos and ask the students to collaborate (mahi tahi) with a partner and write down the symmetry that each design has (this is useful for assessment purposes). Get pairs to have a korero about what they have written with another pair group, then bring the class together for a collective discussion.
- For each logo get students to demonstrate what symmetry the design has by using a mirror, or folding and flipping, and by tracing and rotating. Make a list of symmetries for each design.
- Tell the students to look at their first list and add any information they may have missed. If they do this in a new colour you will have evidence of their initial independent understanding and their new shared understanding.
- If time permits explore how a simple graphic programme, like PowerPoint, can be used to create simple design elements. By copying the element, reflecting or rotating it, then grouping elements together, complex symmetric design can be created.
Dear family and whānau,
This week we are looking at symmetry and at company logos. We appreciate your help by working with your child to find examples of logos in magazines, television commercials or on websites. For homework your child is asked to sketch two logos in their book and describe their symmetries. Ask your student to explain what reflective and rotational symmetries are, using the logos as examples. 