Little Links

To do this activity, the students need to:

• be able to work in millimetres and fractions of millimetres
• understand what π is and how to use the π key on a calculator
• know how to find the diameter of a circle, given the circumference.

Activity

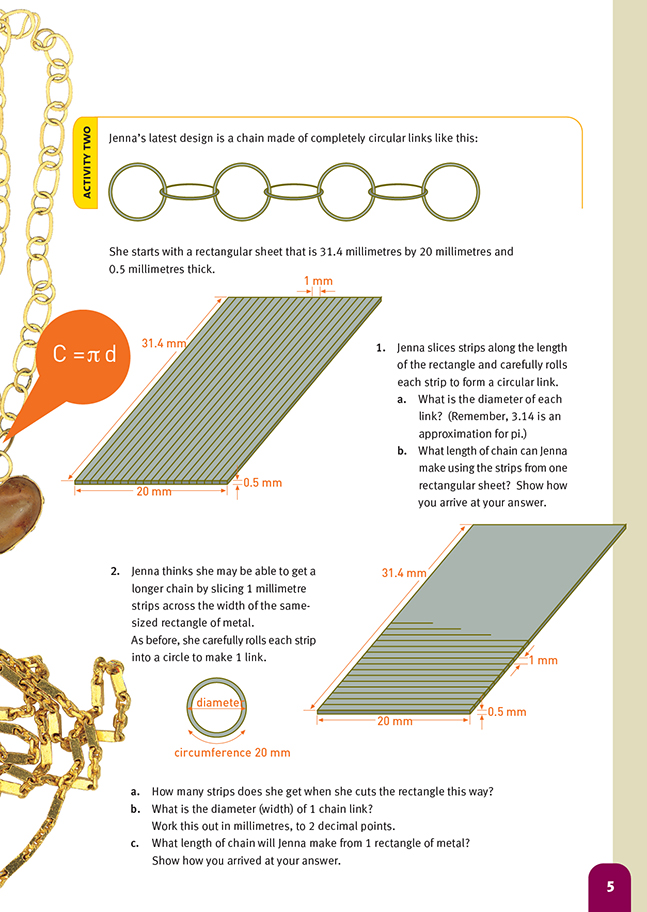
Jenna makes gold and silver chains, cutting narrow strips for the links from small rectangles of metal. The students have to work from the dimensions of the rectangle to calculate the size of the links and the length of the chain that can be made when they are joined. All measurements are given in millimetres.
The students should have completed the Circle Links activity (page 3) before beginning this one. This will ensure that they understand the π relationship between circumference and diameter. Some students may have trouble visualising this task, and for them it could be useful to model it using plastic putty. This would help them to see the way in which the overlap reduces the contribution each additional link makes to the overall length of the chain. If you have good drawing skills, you could illustrate the effect of the overlaps, using a sketch on the whiteboard.
The students are asked to explain how they arrive at their answers. They could do this initially in discussion with other students and then as a written record for sharing and display. This sharing of process is an important skill in mathematics and a requirement of the Mathematical Processes strand of the curriculum.

Answers to Activities

Activity one
1. 5.5 mm. (Each link is formed from a strip that is 15 mm long. The 2 ends of each rectangular link are each 2 mm wide, leaving 15 – 2 x 2 = 11 mm for the 2 sides. 11 ÷ 2 = 5.5.)
2. 50 x 4.5 = 225 mm. (Although each link is 5.5 mm long, when the links are joined, there is an overlap of 1 mm, meaning that each additional link adds 4.5 mm to the total length.)
3. Answers will vary. 50 cm is a reasonable length.  Dividing the length in millimetres by 4.5 (the additional length in millimetres added by each link) will give you the number of links needed.
Activity two
1. a. 10 mm. (When rolled into a circle, the length of each strip, 31.4 mm, becomes the circumference. Circumference = π x diameter; 31.4 = 3.14 x 10
b. 181 mm. (Cutting this way, Jenna gets 20 strips from each rectangle. The first link contributes 10 mm to the length; all the other links add 9 mm because of the overlaps. 10 + 19 x 9 = 181 mm.)
2. a. 31 strips
b. 6.37 mm. (20 ÷ π = 6.37)
c. 167.47 mm, a chain that is slightly shorter. (The first link contributes 6.37 mm to the length; all the other links add just 5.37 mm because of the overlaps. 6.37 + 30 x 5.37 = 167.47 mm.)