Derive multiplication facts from 2, 5 and 10 times tables.
Number Framework Stage 6
Beans collected in film canisters holding ten
Plastic icecream containers.
Using Equipment
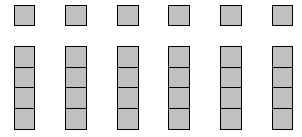
Show the students stacks of five unifix cubes and ask them to confirm the number of cubes in each stack. Show six stacks of five and ask the students to tell you how many cubes there are in total. Discuss their strategies. These should include gathering pairs of five to make tens.
Record the operation as an equation, 6 × 5 = 30.
Problem: What would I have to do to change this into six fours? (take one cube from each stack) How many cubes would I have altogether then? (thirty less six is twentyfour)
This can easily be modelled with the stacks of cubes
Pose similar problems using groupings of five to derive answers to the four and six times tables. For example: 4 × 5 = 20 so what is 4 × 6? 8 × 5 = 40 so what is 8 × 4? Use the canisters of beans to show connections between groupings with ten and nine and eleven.
Pose similar problems using groupings of fi ve to derive answers to the four and six
times tables. For example:
4 x 5 = 20, so what is 4 x 6? (20 add on 4 is 24) 8 x 5 = 40, so what is 8 x 4?
(40 take off 8 is 32)
Use cubes in groups of 10 to show the connections between groupings with 10 and 9
and 11.
Show six stacks of 10 cubes. Ask “How many cubes have I got altogether?” (60)
“How could I write this operation?” (6 x 10 = 60) “What would I do to change this
to six times nine?” (take one cube from each stack) “How many cubes would I have
then?” (60 take off 6 is 54)
.gif)
Pose similar problems, such as:
4 x 10 = 40, so what is 4 x 9? 7 x 10 = 70, so what is 7 x 9?
9 x 10 = 90, so what is 9 x 9? 5 x 10 = 50, so what is 5 x 9?
Derive elevens answers from tens answers.
Model the problems with rows of cubes. For example:
.gif)
Using Imaging
Shielding: Require the students to image the problems by masking the cubes with
large plastic containers. Label each container with the number involved, using
stickies.
For example:
.gif)
Record each operation using multiplication equations.
Appropriate examples might be:
7 x 10 = 70 so what is 7 x 11?
8 x 5 = 40 so what is 8 x 4?
9 x 10 = 90 so what is 9 x 11?
Using Number Properties
Increase the number size so that the students need to address the number properties
rather than relying on images of the materials. Pose the problems as equations, for
example:
5 x 20 = 100 so what are 5 x 19 and 5 x 21?
4 x 30 = 120 so what are 4 x 28 and 4 x 31?
6 x 50 = 300 so what are 6 x 49 and 6 x 52?
7 x 200 = 1 400 so what are 7 x 198 and 7 x 202?