Lining Up

Problem One

The students could find out the mystery number by a process of elimination, but they need to understand how the cards work for question c. The explanation in the Answers should clear up any uncertainty and enable the students to choose their own mystery numbers for a classmate to guess.
You could use the examples in the Answers as a starting point to check whether all the other numbers follow the same pattern. The mystery number in question b, for example, is made up of blue 2 + yellow 8 = 10.
To answer question d, the students only need to be told which cards the mystery number is on. All they need to do is add the top numbers on those cards to find the mystery number. You may want to take the students beyond looking at the top numbers as random numbers to be added together. The cards are actually based on 2 being multiplied by itself (powers of 2). Look at the numbers in the top row of the cards: Red has 1; blue has 2, that is, 1 x 2; green has 4, that is, 1 x 2 x 2; yellow has 8, that is, 1 x 2 x 2 x 2.

Problem Two

This problem is similar to Problem Three, page 3, in that it asks how many different combinations there are of a certain number of items. (On page 3, the items were ice cream flavours and toppings. On this page, the items are letters and digits.)
Ensure that the students know how many letters there are in the alphabet and how many digits there are so that they know how many items they are combining. If the students try to solve this problem using a tree diagram, they will quickly see that the diagram is far too large to be practical. They will have to look for a more efficient method, which in this case is multiplication.
There are 26 choices for the first letter and 26 for the second letter. So altogether there are 26 x 26 = 676 possible letter combinations. There are 10 possible digits for the first number and 10 for the second. This gives 10 x 10 = 100 possibilities. (Alternatively, the numbers run from 00 to 99, which is a total of 100 different numbers.)
This means that for every possible letter combination, you have 100 number combinations. So there must be 676 x 100 = 67 600 possible number plates.
Extension
Ask the students to work out how many different number plates there are using two letters followed by four digits. How many different number plates would there be if there was just one more letter (three letters and four digits)?

Problem Three

Some students may find this problem difficult because the number of boys and girls in a family is expressed differently to the number of brothers and sisters. This is because brothers and sisters are
always expressed in relation to another sibling, whereas expressing the number of boys and girls in
a family is not complicated by a relationship to someone else.
For example: In a family of five girls and two boys, each girl will have four sisters and two brothers
and each boy will have five sisters and one brother. (The number of boys and girls remains
constant.) So the girls will have twice as many sisters as brothers, and the boys will have five times
as many sisters as brothers.
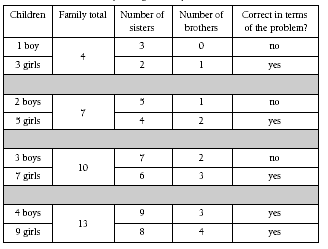
To work out the number of girls and boys in the family in the problem, the students could draw up
a table (see below).
The girls in this family have twice as many sisters as brothers. The minimum number of children in the family for this to be true for each girl is one boy and three girls. (The three girls are the one girl and her two sisters.) The next smallest number of children for this to be true for each girl is two boys and five girls.
The students could continue to calculate the number of children in the family until they find the total that is true for both boys and girls. They could record their results in a table:

Problem Four

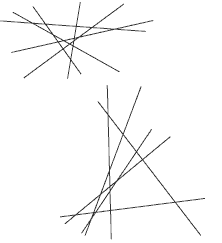
The students are looking for the greatest number of lamp posts for six streets, which means they need to arrange the six streets so there are the greatest number of intersections. You may need to point out to the students that arranging the streets in a conventional right-angled grid will not give the greatest number of intersections.
How many lamp posts can you have if there are four streets? Build this up from the three-street example. If you add one more street, that street can cross all the original three streets. So you get three extra lamp posts or six altogether.

Now try five streets. Starting from the four-street case, you can add another street that will cut all the previous four. This has to add another four lamp posts to give a total of 10. (Of course, from a town planning point of view, this layout may not be very practical. You could use this for a discussion about road planning.)

Now the sixth street can be made to cut each of the other five to give five more lamp posts. At this point, there are 15 lamp posts altogether. There are lots of ways to do this. Two ways are shown in the answers.
This question is similar to Problem Four, page 1. See also Problem Three, page 22.

Hints for Students

1. If you made 6 by adding some of these top numbers, which cards would the 6 be on? How many ways can 15 be made by adding these top numbers? What cards is 15 on?
Can you see a pattern in the top numbers of the cards?
2. How many different letters are there?
How many different digits are there?
How can you find out how many combinations there are of all these letters and digits?
If you are still stuck, look at Problem Three on page 3.
3. Spend some time at first making sure you understand the question.
For example, what exactly does “the girls have twice as many sisters as brothers” mean?
You might find it easier to say “the boys have three times as many sisters as brothers” rather than saying “one-third”.
You could guess and check this one or use a table.
4. Try working upwards from four to five and then to six streets.

Answers to Problems

1. a. 11
b. 10
c. The first number on each card is added to the first number on one or more of the
other cards to give the rest of the numbers on each card. For example, green 4 + red 1 = green 5. Green 4 + blue 2 = green 6. Green 4 + blue 2 + red 1 = green 7. You
can’t have green 8, because no other first numbers add up to 4.
d. Answers will vary, but they will be based on adding the top numbers on the cards
that contain the mystery number.
2. 67 600 (26 x 26 x 10 x 10)
3. 13 children (nine girls and four boys)
4. 15. Two of the ways to show this are: