Techniques for drawing linear graphs are introduced via whole number problem situations where the focus is on the solutions rather than the technique. Only linear equations of the form ax±by=c are graphed by finding two or more points on the line. No attempt is made to link these equations by algebra to the gradient intercept form y=mx+c.
- Find pairs of whole number co-ordinates and use them to draw graphs in problem contexts.
- Link the graphs to formulae of the kind ax±by=c
- Find the nth whole number pairs in a context that solve ax-by=c
Students are introduced to drawing linear graphs related to equations of the type ax±by=c. There is a problem solving focus in the sense that the whole number co-ordinates provide solutions to simple problems even though the graphs have been drawn using continuous variables. Simple linear patterns using a parameter representing the nth term to find relevant x and y values is introduced.
- Graph paper
Session 1
- Introduce the problem:
Mary buys x socks and y ties for $48. A pair of socks costs $3 and a tie $4. What combinations of socks and ties can Mary buy?
One of Polya’s problem solving ideas is to push to the extremes. Here this could mean Mary buys all socks and then Mary buys all ties. - Discuss why this gives 16 pairs of socks, or 12 ties as solutions.
- Discuss how you could show these solutions as points on a graph. (Plot socks on x-axis and ties on y-axis, therefore (16, 0) and (0, 12))
- Discuss whether there are other solutions eg (4, 9). Set up the graph with suitable axes and plot the points. Discuss why connecting the points is sensible. What are other solutions? (The graph shows all 5 solutions at the lattice or “cross” points.
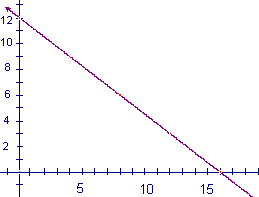
- Discuss what the equation of this graph is. (3x+4y=48)
- If there is room on the same graph solve Mary’s problem if she had $36 dollars to spend and add the equation of the graph (3x+4y=36). Otherwise draw a new graph.
- If there is room on the same graph solve Mary’s problem if she had $72 dollars to spend and add the equation of the graph (3x+4y=72). Otherwise draw a new graph.
- Discuss what the graph of 3x+4y=k would be like. (It would be parallel to the other 3 lines, and its position would depend on the number k.)
Session 2
- Reintroduce the problem:
Mary has $12 to spend on x socks and y ties. A pair of socks costs $3 and a tie costs $4. Mary does not have to spend all her money. What combinations of socks and ties are possible? - Discuss how to graph 3x+4y=12 as in session 1. Then the solution set is all whole number “crosses” on or below 3x+4y=12 as shown in the graph
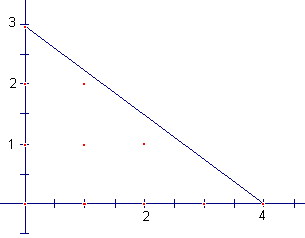
- Discuss the whole number answers to 3x+4y≤12.
- Use graphs to find the whole number solutions to:
3x + 4y ≤ 24
2x + 3y ≤ 12
3x + 5y ≤ 15
4x + 5y ≤ 20
Session 3
- This time Mary has $27 to spend on x socks and y ties. A pair of socks costs $3 and a tie $4.
- Discuss how to graph the solutions. Pushing towards all money spent on socks gives (9,0) as a solution. But pushing towards all money spent on ties gives (0,6 ¾) as a solution. Discuss why this point is undesirable. ((0,6 ¾) does not sit on a lattice point so there are potential problems with accuracy of plotting.) Discuss how buying 1 pair of socks leaves $24 for ties so (1, 6) is a solution. This enables two whole number points to be used to draw 3x + 4y = 27. Graph this to find all the “cross” solutions.
- Solve these equations for whole numbers by drawing graphs. Only one of the end points is easy to find by setting x = 0 or y = 0.
3x + 4y = 28
5x + 2y = 22
5x + 2y = 24
7x + 2y = 32 - Mary has $31 to spend on x socks and y ties. A pair of socks costs $3 and a tie $4. Pushing towards all money spent on socks gives (10 1/3, 0) as a solution. And pushing towards all money spent on ties gives (0,6 ¾) as a solution.
- Discuss why these points are undesirable. If y = 1 does this give a whole number for x? (Yes - so (9, 1) works.)
- Discuss how buying 1 pair of socks leaves $24 for ties so (1, 6) is a solution which enables the two whole number points to be used to draw 3x + 4y = 27.
- Solve these equations for whole numbers by drawing graphs. Neither extreme point can be found by setting x or y = 0.
2x + 3y = 19
3x + 4y = 23;
5x + 2y = 24
7x + 2y = 32
Session 4
- A quiz team is awarded $3 for every correct answer and loses $2 for every wrong answer. At the end of the quiz the team receives $12. If they got x questions right and y questions wrong find all the combinations of right and wrong answers by drawing a graph.
- Discuss why the graph has equation 3x - 2y = 12. Discuss why the smallest possible number of correct answers is equal to 4. So (4,0) is on the graph. Discuss why can x not be equal to 5? (15 -12 = 3, so they had to get 1 ½ question wrong and fraction questions are nonsense.)
- Discuss why can x be equal to 6? (Yes: 18 - 12 = 6, so they had to get 3 question wrong So (6, 2) is on the graph.
- Discuss the developing pattern of points. (4,0), (6, 3), (8, 6), (10, 9)...
- Graph 3x - 2y = 12.
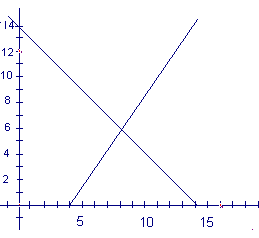
- Suppose the total number of questions was 14.
- Add x + y = 14 to the graph and find out how many correct and incorrect answers there were. (From the intersection of the graphs x = 8, y = 6.)
- In the next quiz a team is awarded $3 for every correct answer and loses $2 for every wrong answer. At the end of the quiz the team receives $24.
- Draw a graph that shows the possible pairs of right and wrong answers.
- If there were 23 questions asked how many answers were right and wrong? Draw another graph to solve this. (14 and 9)
- In another quiz a team is awarded $10 for every correct answer and loses $9 for every wrong answer. At the end of the quiz the team receives $40.
- Draw a graph that shows the possible pairs of right and wrong answers.
- If there were 42 questions asked how many answers were right and wrong? Draw another graph to solve this. (22 and 20)
Session 5
Developing formulae.
- In the previous session a quiz team is awarded $3 for every correct answer and loses $2 for every wrong answer. At the end of the quiz the team receives $12. The solutions were, in order, (4,0), (6, 3), (8, 6), (10, 9) …These are summarized in the table below.
Solution
x
y
1st
2nd
3rd
4th4
6
8
100
3
6
9nth
- Revise finding linear patterns. Then discuss what is the 100th solution. (x = 2 x 100 + 2 = 202, y = 3 x 100 - 3 = 297.)
- Discuss “What is the nth solution?” (x=2n+2, y=3n-3)
- Find formulae for x and y for the 1000th solution and the nth solution for these quiz problems.
- A quiz a team is awarded $4 for every correct answer and loses $2 for every wrong answer. At the end of the quiz the team receives $12.
- A quiz a team is awarded $10 for every correct answer and loses $1 for every wrong answer. At the end of the quiz the team receives $120.
- A quiz a team is awarded $5 for every correct answer and loses $6 for every wrong answer. At the end of the quiz the team receives $15.
- The first whole number solution for 3x-5y=15 is (5, 0). Find the next 3 solutions. ((10,3), (15, 6), (20, 9)). Find the nth solution. (x = 5n, y = 3n - 3)
Extension
Suppose a and b are any whole numbers. What is the first whole number solution for ax-by=ab? ( (b, 0) ) Find the next 3 solutions. ((2b, a), (3b, 2a), (4b, a)) Find the nth solution. (x = bn, y = an - a.)