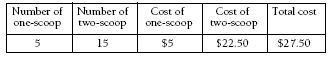These are level 3 number and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (276 KB)
find number of painted faces on 3 dimensional shapes (Problem 2)
use addition and multiplication to solve problems (Problems 3 and 4)
Problem One
The best strategy is to build up the queue as you feed in the information. It is done here in words, although the students might find it easier to use marked bottle-tops or pieces of paper with names on.
i. Only Zoe is between Albert and Ripeka, so you have:
either Albert, Zoe, Ripeka or Ripeka, Zoe, Albert. There is no one between these three shoppers.
ii. Katrina is next to Emil, so you have:
either Katrina, Emil or Emil, Katrina. There is no one between these two shoppers.
iii. There are two shoppers between Ripeka and Emil. There are only five shoppers in the queue, so Emil comes either before or after Albert in the queues you started in i.
Hence you have:
either Emil, Albert, Zoe, Ripeka or Ripeka, Zoe, Albert, Emil.
From ii, Katrina is next to Emil, so you have:
either Katrina, Emil, Albert, Zoe, Ripeka or Ripeka, Zoe, Albert, Emil, Katrina.
The last fact given is that Emil is near the end of the queue, so the order has to be Ripeka, Zoe, Albert, Emil, Katrina. Ripeka is first in line.
The students should check their final answer by making sure that all of the information in the problem has been used and used correctly.
This is a good problem to test the students’ logic. They could also write their own problems about queues. They will see the need to include sufficient information to produce an answer but only just enough to make it unique. (In the problem given, there would have to be two answers if the last fact was not given.)
Problem Two
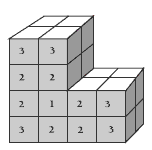
The students will need to work systematically to ensure that they count all the cubes but also that they count each cube only once. It’s probably easier to draw a diagram and label each cube with the number of painted faces. Then they can count all the cubes with one painted face, two painted faces, and so on.
Counting will be quicker if they realise that the model is the same front and back, so they only need to count the painted faces of the cubes on the front of the model and then double these numbers to get the totals.
The students can check their answers by counting the number of cubes in the diagram (24) and then adding all the numbers of cubes that have got one, two, and three painted faces (2 + 12 + 10 = 24). This way, they can be sure that they’ve counted all the cubes.
Problem Three
Students can approach this in various ways and with varying degrees of sophistication. They could use trial and improvement, or they could make their trial and improvement more efficient if they notice that starting with the consecutive number that is one higher than in their previous trial increases the sum by 3. For example, 18 + 19 + 20 = 57 and 19 + 20 + 21 = 60. The sum increases
by 3. How far are they away from 81? 81 – 60 = 21, so they need another 21 in the sum.
21 ÷ 3 = 7, so they need to add 7 to the first consecutive number. This gives 26 + 27 + 28 = 81.
The most sophisticated approach requires students to understand that multiplication is repeated addition. Adding three consecutive numbers is like multiplying the middle number by 3 (because multiplication is repeated addition). It is the middle number that is multiplied by 3 because the first number is one less than the middle number and the last number is one more and they cancel each other out. To find the middle number, divide 81 by 3. 81 ÷ 3 = 27, so the three consecutive numbers are 26, 27, and 28.
You might like to begin by referring to Problem One b on page 7 and then asking the students an easier question. For example, what three consecutive numbers add to 21?
Problem Four
This problem involves finding unknown variables. For students at this level, using a table and trial and improvement are good strategies. They need to make sure that, in each row, the numbers of one- and two-scoop ice creams add up to 20.
When they get to this point in the table, the students should be able to work out the correct answer:
At this point, they are only 50 cents short in the total cost, so they need to add one two-scoop and subtract one one-scoop.
The correct number of ice creams is 4 one-scoops and 16 two-scoops.
Check: (4 x $1) + (16 x $1.50) = $4 + $24 = $28
The students could also work through the problem like this:
If all 20 children had one-scoop ice creams, the total cost would be $20. But if one child had a two-scoop ice cream, the cost would have been $19 + $1.50 = $20.50. In fact, each child who has a two-scoop ice cream pushes the $20 one-scoop bill up by 50 cents. The final bill was $28, which is $8 above $20. $8 is 16 x 50 cents, so 16 children had two-scoop ice creams and four children had one-scoop ice creams.
Check: (4 x $1) + (16 x $1.50) = $4 + $24 = $28
Hints to Students
1. Take each piece of information step by step and build up the queue.
It might be useful to use equipment or draw a diagram to do this.
2. Use equipment if you can’t imagine what is going on by looking at the model, or you could use a diagram.
3. You could find the sums of the two lots of consecutive numbers given in the question (3, 4, 5 and 29, 30, 31). Can you see a pattern?
Why do you think this works?
4. Use trial and improvement and record your results on a table.
Answers to Problems
1. Ripeka
2. a. 2
b. 12
c. 10
3. 26, 27, 28
4. 16