In this unit we look at number patterns from letters and numbers. We use a table of values to help record our thinking. It’s important here to look for the pattern and see how the number of tiles changes from letter to letter.
- Draw the next shape in a pattern sequence
- See how the pattern continues from one shape to the next
- Draw up a table of values.
Patterns are an important part of mathematics. It is valuable to be able to tell the relation between two things in order to predict what will happen and understand how they interrelate.
Patterns also provide an introduction to algebra. The rules for simple patterns can be first discovered in words and then be written using algebraic notation.
Links to Numeracy
This unit provides an opportunity to develop number knowledge in the area of Number Sequence and Order, in particular development of knowledge of skip counting patterns.
Help ākonga focus on the number patterns by discussing the tables showing the numbers of tiles used in each successive letter pattern. Look at those patterns that are made by adding a constant number of tiles onto each successive letter. Highlighting numbers on a hundreds board or using a number line may also be helpful.
Questions to develop strategic thinking could include:
Which number comes next in this pattern? How do you know?
Which number will be before 36 in this pattern? (or another number, as appropriate). How do you know?
What is the largest number you can think of in this pattern? please can you explain your thinking?
Could you make a letter T with 34 tiles? How do you know?
This unit can be differentiated by altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. Specifically, some ākonga may explore the patterns and describe how the shape and number patterns are growing, but may not be ready to predict the next number in the pattern, or how many tiles would be needed to make the nth shape in the pattern. Ākonga could be challenged with number patterns that involve larger numbers. This will encourage them to use a table to explain the number pattern, as drawing or constructing the pattern becomes impractical.
The context of letter patterns can be adapted to recognise diversity and ākonga interests to encourage engagement. Support ākonga to identify and explore other growing patterns in their environment. For example, tukutuku patterns on the walls of the wharenui, or the number of seats on the bus that are occupied as ākonga get onto the bus in pairs.
Te reo Māori vocabulary terms such as letter (reta), tau (number) and tauira (pattern) could be introduced in this unit and used throughout other mathematical learning.
Getting started
Starting with a simple pattern, we build up the level of difficulty and see that it’s necessary to use a table to record what is happening.
Build up the letter ‘I’ using coloured tiles or paper (see the diagram below).
How many tiles do we need for the first ‘I’? The second? The third?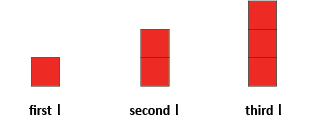
Who can tell me how many tiles we’ll need for the fourth ‘I’?
Can someone come and show us how to make the fifth ‘I’?
How many tiles will we need for the tenth ‘I’? Make it.
What is the number pattern that we are getting?
If we had 11 tiles, which numbered ‘I’ could we make?Now let’s make it a bit harder. Let’s make an ‘I’ by adding a tile to the top and the bottom each time (see diagram).

Repeat the questions from the last ‘I’ problem.
How many tiles do we need for the first ‘I’? The second? The third?
Who can tell me how many tiles we’ll need for the fourth ‘I’?
Can someone come and show us how to make the fifth ‘I’?
How many tiles will we need for the tenth ‘I’? Make it.
What is the number pattern that we are getting?
How many tiles do we add on at each step?
If we had 11 tiles, which numbered ‘I’ could we make?- It was easy to see what was happening in the original ‘I’ problem and to see how many tiles each ‘I’ needed. It wasn’t quite as easy with the second one we did. But what if we had a really difficult pattern? How could we keep track of what’s going on and see how many tiles we need for each letter (reta)?
After korero, suggest the idea of a table. The original ‘I’ problem would give us an easy table. It would look like this:
‘I’ number
1
2
3
4
5
Number of tiles
1
2
3
4
5
What would the table look like where we added two tiles at a time?
Draw up the table with help from the ākonga- Now let the ākonga complete the table for the letter pattern on Copymaster 1. Support ākonga the while they are working and help them by asking leading questions such as:
How did you know how many tiles to use on the fourth ‘L’?
What is the pattern (tauira) here?
Which ‘L’ in the sequence will use 27 tiles? - Bring the class back together and discuss their work.
Tell me what numbers you used to fill the table. (Check that they are correct by counting the tiles.)
What patterns can you see here?
How did you get the number of tiles for one ‘L’ from the one before?
How many tiles would you need for the 10th ‘L’?
If you had 23 tiles, what numbered ‘L’ could you make?
Exploring
For the next three days the ākonga work at three stations continuing different number patterns and building up the corresponding tables. In the first station, the ākonga complete a similar problem to the one in ‘Getting Started’. In the second station the ākonga find a missing shape in the pattern sequence. Finally in the third station ākonga make their own pattern that fits the given table of values. Ākonga could work in three groups that provide tuakana/teina support. At the end of each day, bring them back together to discuss their thinking. Ask them the kind of questions that were used in ‘Getting Started’. Use the tables to discuss the patterns involved and the relation between successive numbers in the sequence.
Day 1
The material for these stations is on Copymasters 1.1, 1.2, 1.3, 1.4. The ākonga continue the pattern and complete the table. Ākonga could continue to use tiles to support their learning.
Day 2
The material for these stations is on Copymasters 2.1, 2.2, 2.3, 2.4. The ākonga find the missing element of the pattern and complete the table. Tiles could be provided for some ākonga who may need to construct the missing element before drawing it.
Day 3
The material for these stations is on Copymasters 3.1, 3.2, 3.3, 3.4. The ākonga make up their own pattern to fit the values in the table. Ākonga could use the tiles to create patterns and count to check that they match the numbers in the table before drawing them on the sheet.
Reflecting
On the final day let the ākonga make up their own patterns using numbers or shapes, instead of letters. They could construct these with tiles first, or by drawing. Encourage ākonga to think of patterns in their environment, for example, tukutuku patterns in the local wharenui or museum. Ākonga should also provide a table to show the number pattern of their number or shape. Some ākonga might want to leave gaps in the patterns of their numbers or shapes. Other ākonga could fill this in when they share their pattern with the class.
When ākonga are sharing their patterns with the class, point out the importance of the table in seeing what the number pattern is.
Dear parents and whānau,
This week in maths we have been exploring number patterns that come from letters, numbers and shapes. Work with your child to fill in the table below for the plus sign shape in the diagram.

| ‘+’number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| number of tiles |
How many tiles would there be in the 4th ‘plus’ shape?
How about the 10th ‘plus’ shape?
Which ‘plus’ in the sequence would you be able to make with 25 tiles?
Exploring and understanding patterns is an important and interesting part of maths. Perhaps you and your child could create another letter, number or shape and explore what number patterns could occur when it is added to. We hope you enjoy doing this. Thank you for your help.