This is a level 3 geometry activity from the Figure It Out theme series.
Click on the image to enlarge it. Click again to close. Download PDF (439 KB)
identify the number of faces, vertices, edges on three dimensional shapes
construct a polyhedron
FIO, Levels 3-4, Theme: Sport, Keeping in Shape, page 8
Interlocking polygon shapes or cardboard, scissor and tape
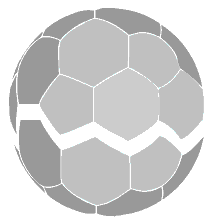
A netball or soccer ball
Plasticine or play dough
A classmate
Activity One
The students will need to use a systematic approach to count the number of faces on the ball. Some may notice that the netball or soccer ball can be divided into two symmetrical halves, which makes the counting easier.
Alternatively, the students could mark each face with chalk as they count. They will find that the ball has 20 hexagonal faces and 12 pentagonal faces. This polyhedron can be described by the notation (6, 6, 5), which means that around each corner are two hexagons (6 sides) and one pentagon (5 sides). This pattern of surrounding each corner with two hexagons and one pentagon gives the “recipe” for building the polyhedron from shapes.
For question 1b, counting the edges and vertices can be a time-consuming exercise. As a more efficient method, the students could think about how many sides of either a hexagon or a pentagon meet at each edge. Two sides are used to make each edge. The polyhedron is made of 20 hexagons and 12 pentagons. This is (20 x 6) + (12 x 5) = 180 sides. Dividing this by two gives the number of edges, 90. A polygon has the same number of sides as corners, so the hexagons and pentagons have a total of 180 corners available to form the vertices of the ball. Three corners are used to form each vertex, so the total number of vertices is 180 ÷ 3 = 60.
Activity Two
Truncated solids are very common in nature. In the case of the soccer ball, the original polyhedron is an icosahedron that has 20 triangular faces. Each corner is chopped through to form a new face.
This creates 12 new faces, the pentagons, while the 20 triangles are transformed into hexagons.
Activity Three
Truncating a cube has a similar result to truncating an icosahedron. The eight vertices are cut through to form eight triangular faces. The six square faces with their vertices removed become octagons. The students can use similar methods to those above to find the number of edges and vertices of the truncated cube. Six octagons and eight triangles have a total of (6 x 8) + (8 x 3) = 72 sides and corners. Two sides make each edge, so the number of edges is 72 ÷ 2 = 36. Two octagons and one triangle meet at each vertex of the truncated cube, using up three corners of the shapes making up the truncated cube; 72 ÷ 3 = 24 is the number of vertices.
Answers to Activities
Activity One
1. a. There are 20 hexagonal faces and 12 pentagonal faces.
b. There are 60 vertices and 90 edges.
2. Practical activity. Teacher to check
Activity Two
1. It becomes a hexagon.
2. 20
Activity Three
1. Octagons and triangles
2. 36 edges and 24 vertices