This problem solving activity has a number and algebra (equations and expressions) focus.

She starts to make different rectangles with them.
She wonders what are the biggest and the smallest perimeters that she can find for rectangles with areas equal to 100 cm2.
- Determine the maximum area of a regular polygon with a given perimeter.
- Appreciate the concept of limit as it applies to the area of regular n-gons and circle that both have the same perimeter.
In this problem students explore the relationship between the perimeter of a rectangle and its area. This includes trying to find the largest and smallest perimeters that can enclose a given rectangular area. To do this students must be able to measure lengths and calculate areas of rectangles. It is helpful if they have also used algebraic equations to solve the problem Peter’s Third String, Number and Algebra (Equations and Expressions), Level 6. The algebra used here is also a useful foundation for further algebraic thinking.
There are seven problems related to perimeter and area.
The first set includes: Peters’ String, Measurement, Level 4; Peters’ Second String, Measurement, Level 5; Peters’ Third String, Number and Algebra (Equations and Expressions), Level 6; The Old Chicken Run Problem, Number and Algebra (Equations and Expressions), Level 6; and the Polygonal String Problem, Number and Algebra (Equations and Expressions), Level 6. These show the non-link between rectangles’ areas and perimeters, and show that among all quadrilaterals with a fixed perimeter, the square has the largest area. The final problem, which looks at the areas of regular polygons with a fixed perimeter, shows that they are ‘bounded above’ by the circle with the same perimeter.
The second set includes: Karen’s Tiles, Measurement, Level 5 and Karen’s Second Tiles, Number and Algebra (Equations and Expressions), Level 6. These problems explore maximum and minimum perimeters for a given area.
Should you wish to explore other shapes with your students, consider triangles or hexagons. For example: can you find two triangles with the same area and perimeter? Or, what is the triangle with given area that has maximum perimeter? The maths required to solve these problems is challenging.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Graphics calculators, graphing software, andd/or graphing paper
The Problem
Karen discovers some old tiles. She starts to make different rectangles with them. She wonders what are the biggest and the smallest perimeters that she can find for rectangles with areas equal to 100 cm2.
Teaching Sequence
- Introduce the problem to the class. Have them consider how they would approach the problem.
- Let the class investigate the problem in any way that they want. Give help, as appropriate, as they begin to record their diagrams and equations.
- Check on group progress as they work. Encourage them to draw large diagrams to show clearly what is going on and to keep a record of their work.
- If a number of students are struggling, a brainstorming or modelling session may help. You may need to remind them of the value of using a table.
- Share the students’ answers. Ensure that they carefully explain their arguments.
- Encourage students to attempt the extension problem. It involves some difficult algebra, which some may find challenging.
Extension
Karen wonders if it's true that two different rectangles can have the same area and the same perimeter?
Mikaere doesn’t think that two rectangles can have the same area and the same perimeter. But he can’t convince Karen of that. Can you?
Solution
This problem can be set up algebraically. From there it can be solved using a table or by drawing a graph.
| Let the rectangles’ variable perimeter be P. If the length of the rectangle is L and the width W (both variables), then | |
| 100 = LW … (1) and P = 2(L + W) … (2). | |
| From equation (1), we can write L in terms of W. | |
| L = 100/W … (3). | |
| Substituting for L in (2) gives us | |
| P = 2(100/W + W) … (4). | |
At this point there are two ways to proceed using a table or graph.
The table method:
W | P |
5 | 50 |
6 | 45.33 |
7 | 42.57 |
8 | 41 |
9 | 40.22 |
10 | 40 |
11 | 40.18 |
12 | 40.67 |
13 | 41.38 |
14 | 42.29 |
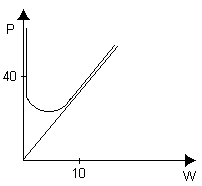
It looks as if the smallest value for P is 40 when W = 10. We should investigate this further by choosing some values closer to 10 (perhaps 9.5, 9.6, 9.7, 9.8, 9.9, 10, 10.1, 10.2, 10.3). This is the actual answer.
The graphical method:
This is much easier if your class has graphics calculators (or a computer that will draw graphs). If not, then your students will have to carefully draw a graph on graph paper. Regardless of the method, it should look like the graph below.
As the result of both sets of work above, we can see that if the area of a rectangle is 100 cm2, then the smallest value of the perimeter is 40 cm when W = 10 cm. You might note that this occurs when the rectangle is a square.
But what is the biggest value that the perimeter can have? It may be easiest to see this from the graph. Clearly as W approaches 0, P approaches infinity. And as W approaches infinity, P also approaches infinity. So P can be as big as we want it to be. There is in fact no biggest value for P.
This understanding requires a good grasp of algebra. Suppose that we have two rectangles with lengths and widths L, W and A, B, respectively. If they have the same are, then
| LW = AB … (1) | |
| on the other hand, if they have the same perimeter, then | |
| L + W = A + B … (2) | |
| Multiplying equation (2) by W we get | |
| LW + W2 = AW + BW … (3) | |
| Substituting for LW from equation (1) we get | |
| AB + W2 = AW + BW … (4) | |
| Rearranging gives | |
| AB – AW = BW – W2 … (5) | |
| Or | |
| A(B – W) = W(B – W) … (5) | |
| Now this factorises to give | |
(A – W)(B – W) = 0 … (6) | |
| From equation (6) we see that either A = W or B = W. | |
Substituting the first of these into equation (1) gives B = L (and A = W), and so both rectangles are the same or it gives A = L (and B = W) and again both rectangles are the same. So it is not possible for two different rectangles to have both the same area and the same perimeter.