This is a level 4 geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (342 KB)
describe patterns using the language of transformation
square grid paper
FIO, Level 4, Geometry, Book One, Kōwhaiwhai, page 14
coloured pencils or felt-tip pens
This activity builds on the ideas of Shifting Shapes (page 13 in the students' book). The students create patterns using single transformations and combinations of transformations.
Kōwhaiwhai are often used as ornamentation on the uncarved heke (rafters) of a wharenui. Unlike carvings, kōwhaiwhai are not normally made by a master artist. However, their intricate, elegant curves require a designer's eye. Today, a cut-out stencil is sometimes used for the repeated design, and the painting is done
as a team project involving young as well as old. All kōwhaiwhai have meanings and are not just ornamental.
You could have your students study the geometry of kōwhaiwhai as a purely mathematical topic but, if possible, you should take them to a building or museum where they can see actual examples. You could ask someone knowledgeable to explain how they were made and what their significance is.
Both questions in this activity involve practical work, and the students may create very different patterns. Some may choose to modify the given designs, while others may try to create something quite different.
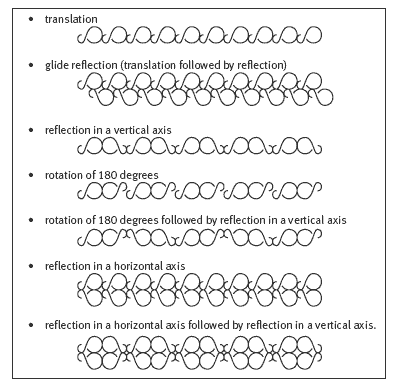
Question 2 says that the three basic transformations can be combined to produce more complex patterns. The complete list of transformations used for kōwhaiwhai is as follows:
Auckland Museum produced an excellent educational kit, kōwhaiwhai Tuturu Māori (PDF, 420KB), which gives a background to the history and significance of kōwhaiwhai, examples of kōwhaiwhai, and an illustrated list of the mathematical transformations used.
- reflection in a vertical axis
- rotation of 180 degrees
- translation
- glide reflection (translation followed by reflection)
- rotation of 180 degrees followed by reflection in a vertical axis
- reflection in a horizontal axis followed by reflection in a vertical axis.
- reflection in a horizontal axis
Answers to Activity
1.- 2. Practical activities. Results will vary.