This problem solving activity has a geometry focus.

Each wheel fits together neatly, like this.
The radius of the largest wheel is 16cm and the radius of the middle-sized wheel is 9cm.
What is the radius of the smallest wheel?
- Apply Pythagoras’ theorem to solve a problem.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, think).
This problem challenges students to work out how to apply Pythagoras’ Theorem to a situation in which the centres of three circles do not lie on a right-angled triangle. Finding a solution involves students in drawing a diagram, connecting points, ascribing letters to points, and applying algebra.
The Problem
Julie stacks three different sized wheels against the shed.
Each wheel fits together neatly, like this.
The radius of the largest wheel is 16cm and the radius of the middle-sized wheel is 9cm.
What is the radius of the smallest wheel?
Teaching Sequence
- Ask the students to write down two things that come into their minds when they first look at the problem.
(circles, radius, circumference, diameter, draw diagram etc.) - List these ideas.
- Look at the list of ideas and discuss which ones they think will be useful in solving the problem.
- You may also like to talk about the skills they have for finding out unknown lengths. This may lead to someone mentioning Pythagoras’ Theorem although its relevance will probably not be apparent. At this stage avoid telling the students that Pythagoras’ Theorem will be needed and leave it as one of the suggestions.
- As the students solve the problem (in pairs) ask questions that require them to explain their reasoning. If they are stuck then you may want to more direct with the Pythagoras prompt.
- Share solutions.
Extension
Can you find a formula for the radius of the smallest wheel in terms of the radii of the other two wheels?
In other words, if you are given the radii of the two larger circles as a and b, can you find c in terms of a and b?
Solution
To apply Pythagoras, the triangles must be found. Let the radius of the smaller wheel be c. We now need three equations.
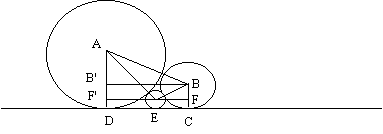
In triangle ABB' , AB = 16 + 9 = 25 and AB' = AD – BC = 16 – 9 = 7,
(BB' )2 = AB 2 – (AB' )2 = 252 – 72 = 576.
In triangle AEF' , AE = 16 + c and AF' = 16 – c, and
(F' E)2 = AE2 – (AF' )2 = (16 + c)2 – (16 – c)2 = 64c,
In triangle BEF, BE = 9 + c and BF = 9 – c, and
FE2 = BE2 – BF2 = (9 + c)2 – (9 – c)2 = 36c.
But BB' = F'F + EF, so
√576 = √64c + √36c
√576 = 8√c + 6<√c
14√c = 24
... √c = 12/7 ... √c = 144/49.
Solution to the Extension
c = ab/(<√a + <√b)2.