This problem solving activity has an algebra focus.
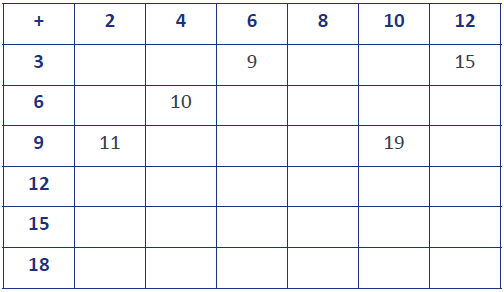
Jo has some squared paper handy. She put the even numbers from 2 to 12 along the top and the numbers 3, 6, 9, 12, 15, 18 down the side. She then started adding the numbers together. As she filled in the numbers she began to see patterns.
Find some patterns for yourself. Use them to complete Jo’s table.
- Continue patterns.
- Describe number patterns.
- Devise and use problem solving strategies (guess and check, make a table, look for patterns).
Patterns are an essential part of mathematics. It is important for students to start looking for them and creating them at the earliest opportunity. This problem challenges students to find patterns in an addition table in horizontal, vertical and diagonal directions. To succeed in this problem, students should be able to add numbers up to 30.
The Problem
Jo has some squared paper handy. She put the even numbers from 2 to 12 along the top and the numbers 3, 6, 9, 12, 15, 18 down the side. She then started adding the numbers together. As she filled in the numbers she began to see patterns.
Find some patterns for yourself. Use them to complete Jo’s table.
Teaching Sequence
- Introduce the problem to the class. Ask them:
What number do you think goes here? Why? - Pose the problem and check it is understood by the students. Discuss ways in which they might show and explain the patterns they see.
- As students work on the problem with a partner or individually, encourage them to record and describe each pattern.
- As a class share the students’ solutions including their descriptions of what is happening in each pattern.
Extension
Look and find out:
- What is the smallest number than appears more than once.
- What is the largest number that appears only once?
- How many times does 15 occur?
Challenge students to create and look for patterns on their own addition table which uses different number patterns across the top and down the side.
Solution
Jo’s completed table is shown below.
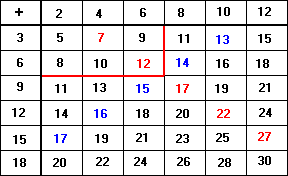
A large number of patterns that can be found.
The horizontal patterns are even and odd numbers. These occur because Jo is adding even numbers together or even numbers plus an odd number.
Diagonal patterns such as the one in red (2, 7, 12 etc.), go up in 5s. This is because the horizontal numbers are increasing in 2s and the vertical numbers in 3s.
Back diagonals such as the one in blue (12, 13, 14, etc.) only increase in 1s. This is because there is an increase of 3 downwards but a decrease of 2 to the left. 3 – 2 = 1. Encourage the class especially to look for patterns that occur in the diagonals.
Solution to the Extension
It’s worth noting that every number outside the red border appears at least twice. This can be seen by looking at the columns and noting the repetitions between them. A quick scan shows that every number inside the red box appears only once. The smallest number that appears more than once must be the smallest number outside the box. This is 11.
The largest number that appears only once must be the largest number inside the orange box. This is 12.
The number 15 only appears in two columns, so it occurs twice.