This problem solving activity has an algebra focus.
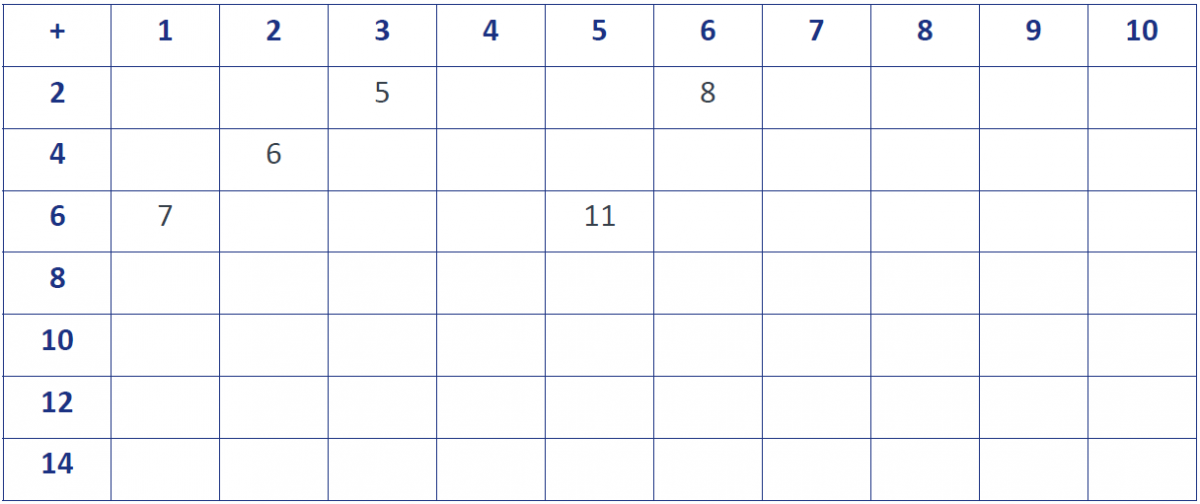
Jim has some squared paper handy. He puts the numbers 1 to 10 along the top and the even numbers down the side. He then starts adding the numbers together. As he fills in the numbers he begins to see patterns.
Find some patterns for yourself. Use them to complete Jim’s table.
- Describe number patterns.
- Add numbers to a total of 24.
Patterns are an essential ingredient of mathematics. Therefore, it is important for students to start looking for patterns and creating them at the earliest opportunity. This problem provides students with the chance to look for patterns in a simple addition exercise. Students should be encouraged to look for number patterns running in horizontal, vertical and diagonal directions in Jim’s table.
The Problem
Jim has some squared paper handy. He puts the numbers 1 to 10 along the top and the even numbers down the side. He then starts adding the numbers together. As he fills in the numbers he begins to see patterns.
Find some patterns for yourself. Use them to complete Jim’s table.
Teaching Sequence
- Introduce the problem to the class. Point to a box in which the answer would be a simple number which your students can make by adding two numbers together. Ask them
What number do you think goes here? Why?
What numbers have we added together to make the new number in Jim's table?
Can you see a pattern? Draw attention to patterns running horizontally, vertically, and diagonally. - Put the suggested numbers into the table.
- And what about here?
- Let the students work on the problem with a partner. Check that they understand what they are supposed to be doing.
- As a whole class share the students’ ideas and solutions. Students should be able to identify patterns and show that they have fully and correctly filled out Jim's table.
- Encourage students to go on to try the Extension problem.
- Discuss the answers that the students get in a class situation. Possibly ask them to make up questions of their own.
Extension
How many times does 4 appear by itself in the body of the table?
How many times does the digit 4 occur in the table?
Which number (as opposed to digit) occurs most in your table?
Solution
Jim’s completed table is shown below.
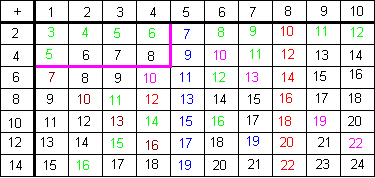
There are a large number of patterns that can be found here, of which a few have been highlighted. These are consecutive numbers (in green) both horizontally and diagonally, odd numbers (in blue), even numbers (in red) and numbers increasing by three (in pink). Encourage students to look especially for patterns that occur in the diagonals.
Solution to the Extension
By searching you can see that there is only 4 in the body of the table. But you can justify this by noting that there can be no 4 to the right of the 4s column or below the 4s row. So the only 4s occur above and to the left of the purple lines. There is only one 4 here.
To see how many times the digit 4 occurs, your students need to understand the difference between a digit (i.e. a symbol) and a number (i.e. a value - such as four ones). This involves a place value discussion. Decide if your students are ready for this.
Going systematically through each column and counting them, you find there are no repeated numbers in the first column (nor any of the other ‘odd’ columns), two in the second, one in the fourth, one in the sixth, one in the eighth, and two in the tenth. This gives a total of seven.
There are several numbers that occur five times. These are 12, 13, 14, 15 and 16.
There are, of course, a lot more questions that you could ask here. For instance, are there more 3s than 4? Which numbers only appear twice? Which digit occurs most?