This problem solving activity has an algebra focus.
Jackson explores the answers you get when you add consecutive numbers together. He systematically records them like this:
For example: 1 + 2 = 3, 2 + 3 = 5, 3 + 4 = 7, 4 + 5 = 9, etc. He calls these the sum of two consecutive numbers.
Using his method, write down some of the sums of three consecutive numbers. One is done for you.
Write down some more. 1 + 2 + 3 = 6.
He decides to find out whether 36 can be written as the sum of two, three, four or five consecutive numbers.
He uses the following table to record his information.
Put some more numbers into their correct columns.
Using the information from Jackson’s table, write some generalisations that he could use to make a quick test to see whether 36 is the sum of of two, three, four or five consecutive numbers.
Choose any number of your own less than 50. Check whether it is the sum of two, three, four or five consecutive numbers.
Extend Jackson’s table to include sums of six and seven consecutive numbers.
Explore all the numbers less than 50 that cannot be written as sums of consecutive numbers.
- Describe a rule for the general term.
- Devise and use problem solving strategies to explore situations mathematically (be systematic).
One of the important parts of this problem is seeing patterns. The first step is to be able to describe the pattern in words. The second step is to find an algebraic expression for the pattern. Mathematics differs from other disciplines in that it must justify the patterns that it sees. Expressing the pattern in an algebraic form is a useful first step to this justification.
The lowest level of this justification is showing that all the data fits the pattern. Every number in a data set should be checked to see that it does satisfy the pattern. Then you must justify that every member of the set satisfies the pattern, even the numbers that aren't yet listed. This is more difficult but it is something that students should be encouraged to try as it is an essential part of mathematics.
The patterns referred to in this problem are called conjectures. Justification is also called proof.
The Problem
Jackson explores the answers you get when you add consecutive numbers together. He systematically records them like this:
For example: 1 + 2 = 3, 2 + 3 = 5, 3 + 4 = 7, 4 + 5 = 9 etc.
He calls these the sum of two consecutive numbers.
Using his method, write down some of the sums of three consecutive numbers. One is done for you. Write down some more. For example: 1 + 2 + 3 = 6.
He decides to find out whether 36 can be written as the sum of two, three, four or five consecutive numbers. He uses the following table to record his information. Put some more numbers into their correct columns.
Using the information from Jackson’s table, write some generalisations that he could use to make a quick test to see whether 36 is the sum of of two, three, four or five consecutive numbers.
Choose any number of your own less that 50. Check whether it is the sum of two, three, four or five consecutive numbers.
Extend Jackson’s table to include sums of six and seven consecutive numbers.
Explore all the numbers less than 50 that cannot be written as sums of consecutive numbers.
Teaching Sequence
- Tell the students that today’s problem will be revealed in parts.
- Write 1+ 2 = 3 on the board
Ask: What do you think the next line could be? - Write the rest of the two consecutive sums on the board.
How could we describe these equations? (sums of two consecutive numbers)
Who could give me a sum of three consecutive numbers? Any more? - Give the problem to pairs of students to continue with.
- As the students work ask questions that focus on their search for patterns:
What can you tell me about the numbers in the table?
Can you see any patterns?
Will these patterns continue for ever?
Can you think of a way to describe the pattern using general terms? - Share solutions.
- What can you say about numbers that are not the sum of consecutive numbers?
Extension
Are there some numbers that can be written both as the sum of two consecutive numbers and as the sum of three consecutive numbers?
Can you justify the patterns that you found above?
Solution
- 2 + 3 + 4 = 9; 3 + 4 + 5 = 12; …
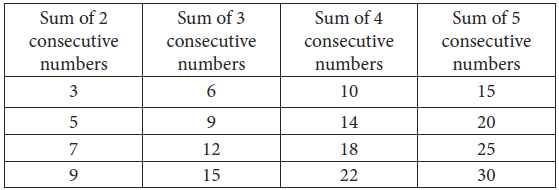
Some further additions of this table may be:
Sum of 2 consecutive numbers | Sum of 3 consecutive numbers | Sum of 4 consecutive numbers | Sum of 5 consecutive numbers |
3 | 6 | 10 | 15 |
5 | 9 | 14 | 20 |
7 | 12 | 18 | 25 |
9 | 15 | 22 | 30 |
11 | 18 | 26 | 35 |
13 | 21 | 30 | 40 |
Some interesting observations are:
- the sums of two consecutive numbers are all odd.
- the sums of three consecutive numbers are all divisible by 3.
- the sums of four consecutive numbers start at 10 and increase by 4 each time.
- the sums of five consecutive numbers start at 15 and increase by 5 each time.
- each column is ‘headed’ by members of the triangle number sequence.
Suppose the table is redrawn:
n | Sum of 2 consecutive numbers | Sum of 3 consecutive numbers | Sum of 4 consecutive numbers | Sum of 5 consecutive numbers |
1 | 3 | 6 | 10 | 15 |
2 | 5 | 9 | 14 | 20 |
3 | 7 | 12 | 18 | 25 |
4 | 9 | 15 | 22 | 30 |
5 | 11 | 18 | 26 | 35 |
6 | 13 | 21 | 30 | 40 |
7 | 15 | |||
Some Patterns
- The two consecutive sums’ column gives 2n + 1.
- The three consecutive sums’ column gives 3n + 3 = 3(n + 1).
- The four consecutive sums’ column gives 4n + 6 = 2(2n + 3).
- The five consecutive sums’ column gives 5n + 10 = 5(n + 2).
- 36 cannot be made from two consecutive numbers since it is even.
- 36 can be made from three consecutive numbers since it is divisible by 3 (here n = 11).
- If 36 can be made from four consecutive numbers, then from III we see that
2(2n + 3) = 36. Hence 2n + 3 = 18 or 2n = 15. - As there is no whole number that satisfies this condition, 36 cannot be the sum of four consecutive numbers.
- 36 cannot be made from five consecutive numbers, as all of these are multiples of 5.
We leave this to you.
n | Sum of 6 consecutive numbers | Sum of 7 consecutive numbers |
21 | 28 | |
27 | 35 | |
33 | 42 | |
39 | 49 | |
M | M |
The patterns here are 6n + 15 and 7n + 21, respectively.
Numbers that cannot be made are 1, 2, 4, 8, 16, 32, 64 i.e. all the numbers from the form 2n.
Solution to the Extension
There are numbers that are both the sums of two consecutive numbers and the sums of three consecutive numbers. You only have to find an odd number greater than 2 that is divisible by 3. For instance 9 and 15 are both sums of two consecutive numbers and three consecutive numbers.
We’ll justify the fact that numbers of the form 4n + 6 are the sum of 4 consecutive numbers. All other patterns can be justified in a similar way.
Suppose N = 4n + 6 and n > 0. Then this can be rewritten as N = n + (n + 1) + (n + 2) + (n + 3). So every N > 6 of the form 4n + 6 can be written as the sum of four consecutive sums.
The tables in this problem can be generated using a spreadsheet.