Te Kete Ipurangi Navigation:

Te Kete Ipurangi
Communities
Schools

Te Kete Ipurangi user options:

Level Three > Geometry and Measurement

Inside Out

Keywords:
Purpose: 

This is a level 3 geometry activity from the Figure it Out series.

Achievement Objectives:

Achievement Objective: Classify plane shapes and prisms by their spatial features.

Specific Learning Outcomes: 

investigate internal angles of polygons

Required Resource Materials: 
FIO, Level 3-4, Geometry, Inside Out, page 5
protractor
cardboard or paper
scissors
ruler
photocopy of enlarge triangles and quadrilaterals from student book
Activity: 

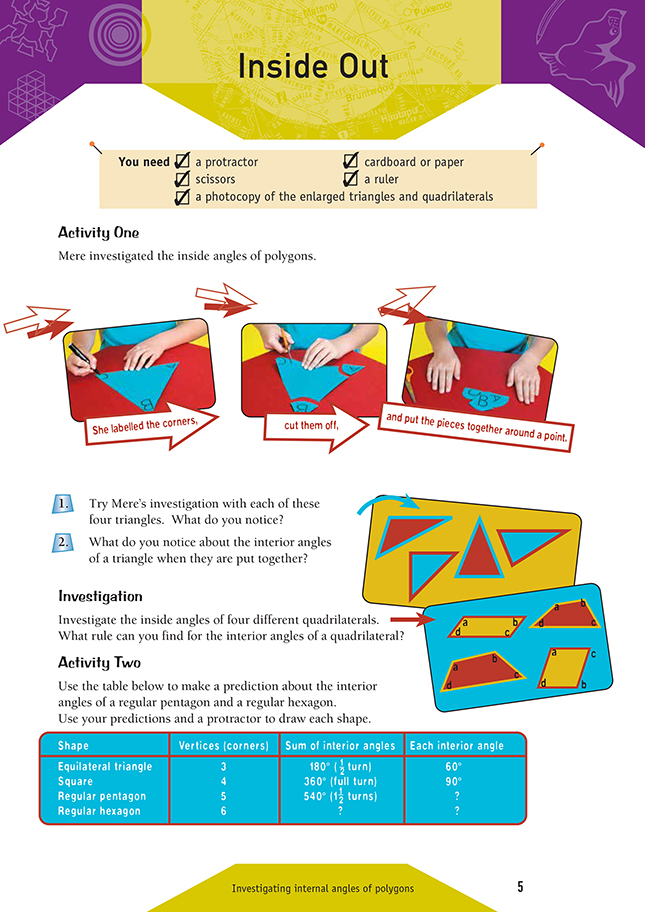
Activity One

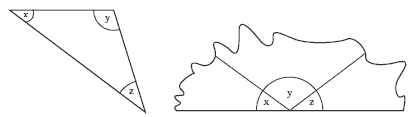
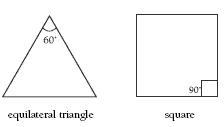
For this activity, you may need to remind the students that the sum of the angles in a straight line is 180° and the sum of the angles in a circle is 360°. This practical task is a very useful way for the students to discover that the sum of the interior angles of a triangle always equals 180°. The students could tear off the corners so that they can clearly recognise the angle originally taken from the triangle.

 

act1.
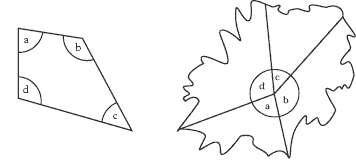
Investigation
Through this investigation, students should discover a similar proof for the sum of the angles of a quadrilateral. They should draw a range of different quadrilaterals (square, rhombus, trapezium, and so on), label and tear off each of the corners, and place them together to show that they form a revolution (360°).
 

invest.

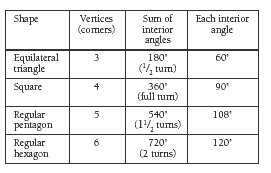
Activity Two

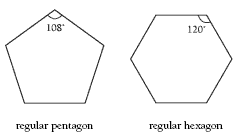
In this activity, students use the sum of the interior angles of a triangle and of a square to find the size of each interior angle of a pentagon and a hexagon. The pattern is that each additional vertex adds another 180° to the sum of the interior angles. Students then use this information to draw the shapes using protractors. After the students have drawn the pentagon and hexagon, they could check the sum of the interior angles by using the same method they used for the triangle and quadrilateral.
Notice that the angles of the pentagon add up to 540° (360° + 180°). This is a full circle plus a semicircle. However, there is no way of combining the individual pieces to form a full circle plus a semicircle. The hexagon yields 720°, which is two full circles.

This activity will help the students when they create tessellations (see page 6 of the student booklet) and explore why certain regular shapes tessellate and others do not.

Answers to Activity

Activity One
1. The pieces of a triangle fit together to form a semicircle. The sum of the angles is 180°.
2. They always add up to 180°.
Investigation
The interior angles add up to 360°.
Activity Two
table.

The shapes are:

shapes.

shapes.


Similar Resources

Fitness

This unit examines regular tessellations, that is, tessellations that can be made using only one type of regular polygon, and semi-regular tessellations, where more than one type of regular polygon is involved. Students are required to investigate what properties tessellating shapes must have in order to cover the plane with no gaps or overlaps.

Tiling

This is a level 3-4 geometry strand activity from the Figure it Out series.

To the Wire

These are level 3 number, geometry, and statistics problems from the Figure It Out series.

Precision Flying

This is a level 4 geometry strand activity from the Figure It Out series.

Alien Action

This is a level 4 geometry strand activity from the Figure It Out series.