This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (231 KB)
find factors of numbers
classmate
multilink cubes or square dot paper (optional, see copymaster))
The students will probably have worked with sets of factors earlier in the students’ book, for example, on pages 12–13. Encourage them to work systematically to make sure that they find all the factors. They can do this by trying to divide their whole number by each number from 1 up to see whether it divides the whole number evenly and therefore is a factor. For example, to find the factors of 16:
16 ÷ 1 = 16
16 ÷ 2 = 8
16 ÷ 3 = 5 remainder 1
16 ÷ 4 = 4
16 ÷ 5 = 3 remainder 1
16 ÷ 6 = 2 remainder 4
16 ÷ 7 = 2 remainder 2
16 ÷ 8 = 2
(The students should be able to do these calculations mentally.) So 1, 2, 4, and 8 are factors of 16. Students only need to try the numbers up to half the number for which they are finding the factors. Numbers greater than half will not divide evenly.
Investigation
In this investigation, the students will be working with numbers that they are familiar with. They will organise data in a systematic way, highlight the significant features, and then see what insights emerge. You can also use the investigation to reinforce the terms prime numbers, composite numbers, rectangular numbers, and square numbers.
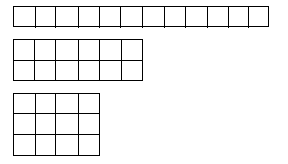
A prime number has only two factors because it is divisible only by 1 and itself. A composite number has more than two factors and can be represented by square or rectangular patterns. For example, 9 has three factors, 9, 3, and 1. It is a square number and a rectangular number. It can be represented as:
or 12 is a rectangular number. Its factors are 1, 2, 3, 4, 6, and 12. It can be represented as:
or
12 is a rectangular number. Its factors are 1, 2, 3, 4, 6 and 12. It can be represented as:
As the students begin this investigation, encourage them to explore square and rectangular patterns with concrete materials (for example, linked cubes) or diagrams (for example, squared paper).
They could put the results in a table and see what they can find out about each of the numbers with two factors, three factors, and so on
Ideas from the students will vary. Encourage them to give appropriate explanations and to record generalisations. In general, square numbers seem to have an odd number of factors, while numbers with four, six, and eight factors are rectangular. Prime numbers have only one rectangular array. Numbers with four factors have two types of rectangular array: 8 has 1 x 8 and 2 x 4. Numbers with six factors have three rectangular arrays: 20 has 20 x 1, 10 x 2, and 5 x 4. Numbers based on a multiple of 12, such as 24 and 36, will have more than six factors because 12 itself already has six factors.
Encourage the students to extend the investigation further. Further questions may be posed by you or by the students themselves. For example:
“Find a number with seven factors (64 is one).”
“How many of the first 100 numbers are prime?”
“6 = 3 + 2 + 1. This is a perfect number because it is equal to the sum of its other factors. Find the next perfect number.” (28)
“Investigate the product of all the factors of a number. (For example, for the factors of 12:
12 x 6 x 2 x 4 x 3 x 1 = 1 728
= 123).”
Answers to Activity
1: 1
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
7: 1, 7
8: 1, 2, 4, 8
9: 1, 3, 9
10: 1, 2, 5, 10
11: 1, 11
12: 1, 2, 3, 4, 6, 12
13: 1, 13
14: 1, 2, 7, 14
15: 1, 3, 5, 15
16: 1, 2, 4, 8, 16
17: 1, 17
18: 1, 2, 3, 6, 9, 18
19: 1, 19
20: 1, 2, 4, 5, 10, 20
21: 1, 3, 7, 21
22: 1, 2, 11, 22
23: 1, 23
24: 1, 2, 3, 4, 6, 8, 12, 24
25: 1, 5, 25
26: 1, 2, 13, 26
27: 1, 3, 9, 27
28: 1, 2, 4, 7, 14, 28
29: 1, 29
30: 1, 2, 3, 5, 6, 10, 15, 30
31: 1, 31
32: 1, 2, 4, 8, 16, 32
33: 1, 3, 11, 33
34: 1, 2, 17, 34
35: 1, 5, 7, 35
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Investigation
Prime numbers have only two factors, themselves and 1.
Prime numbers between 1 and 36 are: 2, 3, 5, 7, 11, 13,
17, 19, 23, 29, 31.
3 factors: 4, 9, 25 (prime numbers squared, plus the number itself and 1)
4 factors: 6, 8, 10, 14, 15, 21, 22, 26, 27, 33, 34, 35
(one rectangular array, plus the number itself and 1)
5 factors: 16 (fourth power of the prime number 2)
6 factors: 12, 18, 20, 28, 32 (two rectangular arrays, plus the number itself and 1)
8 factors: 24, 30 (three rectangular arrays, plus the number itself and 1)
9 factors: 36 (square number)