In this large range of activities some basic concepts in algebra are developed. The intention of this unit is not to teach skills in isolation, but rather to use each activity for developing all the concepts, with opportunities for discussion and consolidation.
- Solve linear equations.
- Describe a linear relationship between two variables in words and as an equation.
- Make a table of one variable against another.
- Use a graph to find the value of y, given x, and x, given y.
The concept of a variable is a difficult one for students to grasp. As maths teachers we often refer to a letter symbol as a variable, when sometimes we mean an unknown specific value, sometimes a generalised unknown, and sometimes we really do mean a variable.
At level 4 students will have constructed Cartesian graphs of integer values and will have solved simple linear equations, but are unlikely to have seen the connection between the two. Graphs provide an accessible visual representation of the relationship between two variables. By using graphs and equations of the same context to find a number of specific values of variables, students will gain an understanding of how equations can be used to represent relationships.
Solving equations is often taught as an algorithm, whereas in this unit students are encouraged to explore a variety of approaches that will develop understanding of what solving equations actually means.
For a structured situation, finding a rule for the general term often causes real difficulties for students. They often see the iterative rule that gives the value of a member of a sequence, given the previous term (e.g. add 3 matches) but are unable to find the general relationship between one variable and the other (e.g. 3 times the number of squares plus 1). The traditional approach of attempting to teach students to interpret tables often results in them learning rules without understanding. The alternative approach used here makes use of the geometry of physical situations to find relationships. As different students will view the geometry in different ways, this gives rise to equivalent expressions which can be used to explore manipulation of algebraic expressions.
Here is a large range of activities that can be used for developing some basic concepts in algebra. Students often complain that they cannot see the point of learning algebra so all of the teaching of skills here is placed within contexts. The intention of this unit is not to teach skills in isolation, but rather to use each activity for developing all the concepts. It is not suggested that this unit should replace the skills practice traditionally used in the teaching of algebra. It does, however, provide the opportunities for discussion and development of concepts. As each learning outcome is explored there will probably be need for consolidation through more traditional exercises. With the first activities one will probably not wish to explore all aspects with the whole class, but the possibility is there for extending individuals. It would also be appropriate to use the first activity for diagnostic assessment.
- Rectangular blocks
- Counters
- Matchsticks or toothpicks
This unit of work is built around 5 algebra activities or problems. These are:
-
Seating Arrangements
-
Overlapping Squares
-
Matchstick Cubes
-
Christmas Trees
-
Waitati Taxis
For each activity a possible sequence for students to follow is:
- Physically model the situation whenever possible. Otherwise use drawings / diagrams.
- Make a table of one variable against the other (e.g. matches vs triangles)
- Draw a line graph using Cartesian coordinates.
- Interpret the graph both ways (How many matches for 3 triangles? How many triangles for 13 matches?)
- Extrapolate and recognise problems with using a graph to extrapolate a long way.
- Interpolate and recognise accuracy problems when non-integer solutions are allowed.
- Describe the rule in words. Move from rules like Add 2 to Twice the number of triangles plus 1
- Describe the rule as an equation (e.g. m = 2t + 1 )
- Find equivalent expressions (e.g. 3t – (t – 1) = 2t + 1)
- Evaluate expressions by substitution (e.g. 2t + 1 when t = 5)
- Solve equations (eg 13 = 2t + 1)
Each activity is initially presented as a problem for students to solve. Instructions relating to the 11 ideas above that teachers may give students are underlined and further scaffolding questions are in italics. As stated earlier it is not suggested that all the learning outcomes should be taught during each activity, therefore not all the instructions should be given to all the students. If the first activity is to be used for diagnostic assessment then most of the instructions can be worked through to find what the students are capable of. In subsequent activities one or more of the instructions may be focused on for active teaching, but other instructions may be given, either for consolidation of learning or as extension.
Activity 1: Seating Arrangements
Rectangular tables are joined together for banquets as in the following diagram of 3 tables.
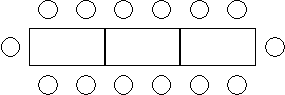
How many people can sit around a row of 9 tables?
How many tables would be needed for a party of 30 people?
A giant street party has 49 tables in a row. How many people can sit round this?
My street has 258 people living in it. How long would the row of tables need to be?
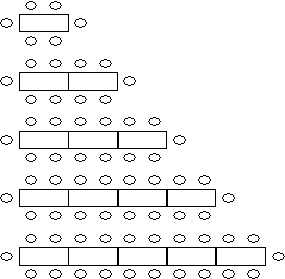
What does a block represent?
What does a counter represent?
Where can the people sit round this arrangement of tables?
|
Tables |
People |
|
1 |
6 |
|
2 |
10 |
|
3 |
14 |
|
4 |
18 |
|
5 |
22 |
What should be the heading of the first column?
What should be the heading of the second column?
How many people can sit around 2 tables?
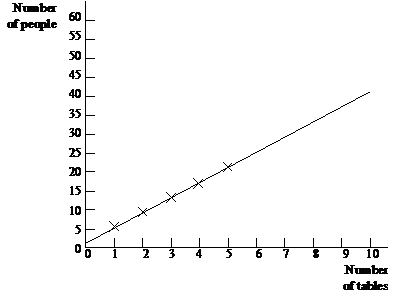
What should be the label on the horizontal axis?
What should be the label on the vertical axis?
Where should you put the numbers on the horizontal axis?
Can we start each axis at zero?
Students’ previous experience of graphs is often just in statistics where they have drawn bar graphs. They therefore often want to place number labels between lines rather than on them.
Do you have the same gap between each number on your horizontal axis?
Students are not always aware of the need for consistent scale.
Approximately how high does the vertical axis need to go? If there were 6 people around every table how many people would there be for 10 tables? Will the vertical axis need to be taller or shorter than this?
If we use one square per person the graph will be VERY tall and skinny. How can we make the graph fit on the page?
Students who realise the need for consistent scale often think they need the same scale for both axes.
For 2 tables how many people are there? Where should this point go?
Can you draw a straight line through your points?
If one of your points is not on the straight line, what does this suggest?
Students will often want to put a dog leg in their graph at (1,6) so that the line goes through (0,0). They should be encouraged to draw one straight line as we are using the line to show the relationship between people and tables.
Where is the point representing the number of people for 9 tables? Can you mark this on the line? Can you trace across to the vertical axis to find how many people?
Where is the point representing the number of tables for 30 people? Can you mark this on the line? Can you trace down to the horizontal axis to find how many tables?
No. We will have to find another way to solve this problem. We could draw a bigger graph but perhaps there is a better way.
Students will often reply, “Plus 4 each time you add a table” but they need to find the relationship.
Show me the people at the head and foot of the table. How many people is this?
Show me the people at the sides of the table.
For 1 table, how many people are at the sides? For the total number of people at the table what do we have to add?
For 2 tables, how many people are at the sides? How many lots of 4 is this? For the total number of people at the table what do we have to add? For 3 tables, how many people are at the sides? How many lots of 4 is this? For the total number of people at the table what do we have to add? For any number of tables, how many people are at the sides? How many lots of 4 is this? For the total number of people at the table what do we have to add?
If students have written a relationship like, “Number of people equals number of tables times 4 plus 2 extra” then writing an equation is not hard. They should be encouraged to treat a symbolic equation as shorthand.
What letter shall we write instead of “number of people”?
What letter shall we write instead of “number of tables”?
When students write equations like p = t x 4 +2, affirm that this is correct but that it is conventional to write p = 4t + 2
For 1 table what does Joneen’s equation say the number of people is? For 1 table what does Melissa’s equation say the number of people is?
For 3 tables what does Joneen’s equation say the number of people is? For 3 tables what does Melissa’s equation say the number of people is?
For 10 tables what does Joneen’s equation say the number of people is? For 10 tables what does Melissa’s equation say the number of people is?
Why has Joneen written the rule as p=4t+2?
Why has Melissa written the rule as p=6+4(t-1)?
Can you explain why 4t + 2 is the same as 6 + 4(t-1)? Look for answers like “we have 4 lots of t and 4 lots of negative 1, and 6 plus 4 lots of negative 1 is 2.”
Write the equation for me.
What does t represent?
How many tables are there this time?
What should we write instead of t?
Can you calculate 4 x 9 + 2?
Look at your graph. How many people does it say can fit around 9 tables?
Write the equation for me.
What does t represent?
How many tables are there this time?
What should we write instead of t?
Can you calculate 4 x 49 + 2?
Write the equation for me.
What does p represent?
How many people are there this time?
What should we write instead of p?
If 258 = 4t +2, how could we find t?
The most obvious strategy is ‘guess and check’ and this should be accepted initially.
How could we work out the value of t without guessing?
An intermediate stage between Guess and Check and formal symbolic algebra is the use of Box Diagrams:
|
t |
t |
t |
t |
2 |
|
258 |
||||
By representing the magnitude of t as a length, the diagram can be operated on in the same way as the symbolic equation, but we have a visual representation to make it meaningful.
If I removed this 2 box and 2 from the 258, what diagram would result?
If 4 lengths of t are equal to 256, how long is one length of t?
|
t |
|
64 |
Rather than teach rules for manipulating symbolic equations, students can abstract the rules themselves through operating on box diagrams, then visualising box diagrams.
If I had drawn a box diagram for this equation, what would it look like?
What would be the first thing I should do to the box diagram?
How would I write the equation that represents this?
Students should always be expected to check their solution by substituting back into the equation.
p = 4 x 64 +2
p = 258
- Use blocks and counters to represent 1 table, 2 tables, etc up to 5 tables
- Make a table showing the number of people versus the number of tables
- Draw a graph showing the number of people versus the number of tables for up to 10 tables
- Use your graph to find how many people can sit around a row of 9 tables. Use your graph to find how many tables would be needed for a party of 30 people.
- Can you use your graph to find how many people fit around 49 tables?
- What is the relationship between the number of people and the number of tables?
- Write your rule as an equation
- Joneen has written p = 4t + 2 and Melissa has written p = 6 + 4(t-1). Who is correct?
- Use your equation to find how many people can sit around 9 tables, 49 tables.
- Use your equation to find how many tables are needed for 258 people.
Further Activities
Many activities can be approached in the same way as above. A few are described below. They have been sequenced so that skills are developed further and opportunities for additional teaching points arise naturally. Included are the possible instructions to students for each activity, but the approach and scaffolding questions are directly parallel to the first activity. Only where learning outcomes were not addressed in the first activity is a more complete description given.
Activity 2: Overlapping Squares
Matchsticks are used to make a pattern of overlapping squares as in the following diagram of 3 squares.
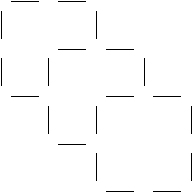
How many matchsticks are required for 8 squares?
How many squares could be made with 38 matchsticks?
How many matchsticks are required for 81 squares?
How many squares could be made with 134 matchsticks?
- Use matches to represent 1 square, 2 squares, etc up to 5 squares.
- Make a table showing the number of matches versus the number of squares.
- Draw a graph showing the number of matches versus the number of squares for up to 10 squares.
- Use your graph to find how many matches are used for 7 squares. Use your graph to find how many squares could be made with 56.
- Can you use your graph to find how many matches are used for 33 squares?
- What is the relationship between the number of matches and the number of squares?
Show me the matches you have to add on when you change the diagram from one to two squares.
Show me the matches you have to add on when you change the diagram from two to three squares.
Show me the matches you have to add on when you change the diagram from three to four squares.
How many matches are there for each square you are adding?
Can you make the first square with 6 matches? How many extra matches are needed for the first square?
So we need two extra matches for the first square and how many for every square? What is the connection between the number of squares and the number of matches?
- Write your rule as an equation.
- Julie has written m = 6s + 2 and Denise has written m = 8s – 2(s – 1). Who is correct?
- Use your equation to find how many matchsticks are required for 8 squares, 81 squares.
- Use your equation to find how many squares could be made with 38 matchsticks, 134 matchsticks.
Activity 3: Matchstick Cubes
Matchsticks are used to make a pattern of cubes as in the following diagram.

How many matchsticks are required for a row of 5 cubes?
How many cubes could be made with 39 matchsticks
How many matchsticks are required for a row of 42 cubes?
How many cubes could be made with 134 matchsticks?
- Use matches to represent 1 cube, 2 cubes, etc up to 5 cubes.
- Make a table showing the number of matches versus the number of cubes.
- Draw a graph showing the number of matches versus the number of squares for up to 10 cubes.
- Use your graph to find how many matches are used for 7 cubes. Use your graph to find how many cubes could be made with 49 matches.
- Can you use your graph to find how many matches are used for 28 cubes?
- What is the relationship between the number of matches and the number of cubes?
- Write your rule as an equation.
- Julie has written m = 9 + 5(x-1), Melissa has written m = 3x + 4 +5x, Joneen has written 9x – 4(x-1) and Denise has written m = 4 + 5x. Who is correct?
- Use your equation to find how many matchsticks are required for 5 cubes, 42 cubes.
- Use your equation to find how many cubes could be made with 39 matchsticks, 134 matchsticks.
Activity 4: Christmas Trees
Every year in December Bruce buys a 1.5m tall live Christmas tree then, on New Year’s day, plants it in his garden. Over the years he has measured his trees and found that they grow 0.5m every year.
How tall will a tree be after 6 years?
How many years until a tree is 6m tall?
How tall will a tree be after 3.5 years?
How many years until a tree is 8.6m tall?
- Make a table showing the height of tree versus the number of years old
- Draw a graph showing the height of tree versus the number of years old for up to 10 years
- Use your graph to find how high a tree is after 6 years. Use your graph to find how many years until a tree is 6m tall.
- Can you use your graph to find how high a tree is after 3.5 years?
Where is the point representing the height after 3.5 years?
Can you mark this on the line?
Can you trace across to the vertical axis to find the height?
Is the height an exact number of metres?
Can you tell me exactly what the height is?
This is a situation where non-integer solutions are meaningful. Graphs can now give answers that are only approximate. -
What is the relationship between the height of a tree and its age?
How much does a tree grow in one year? What is its total height after 1 year?
How much does a tree grow in 2 years? How many lots of 0.5m is this? What is its total height after2 years?
How much does a tree grow in 3 years? How many lots of 0.5m is this? What is its total height after 3 years?
How much does a tree grow in 4 years? How many lots of 0.5m is this? What is its total height after 4 years?
How much does a tree grow in x years? How many lots of 0.5m is this? What is its total height after x years? - Write your rule as an equation.
- Use your equation to find how high a tree is after 6 years, 3.5 years.
- Use your equation to find how old a tree is when it is 6m tall, 8.6m tall.
Activity 5: Waitati Taxis
The Waitati Taxi Company charge a flag fall of $2.50, then an additional $1.70 per kilometre.
What is the cost of a 4km taxi ride?
How far can you travel for $11?
What is the cost of an 8.6km taxi ride?
How far can you travel for $40?
- Make a table showing the cost versus the distance travelled.
- Draw a graph showing the cost versus the distance travelled for up to 10km.
- Use your graph to find the cost of a 4km taxi ride. Use your graph to find how far can you travel for $11.
- Can you use your graph to find the cost of a 8.6km taxi ride?
- What is the relationship between the cost and the distance travelled?
- Write your rule as an equation.
- Use your equation to find the cost for 4km, 8.6km.
- Use your equation to find the distance travelled for $11, $40.