Ka āta tirohia te whakaatu i ngā putanga e taea ana i tētahi horopaki tūponotanga ki te hoahoa rākau, me te whakamahi hoahoa rākau hei tātai tūponotanga. I takea mai tēnei kōwae ako i te kōwae ako reo Ingarihi Probability Trees. E rua wiki pea te roa o tēnei kōwae ako.
- ka whakamahi hautau, ōwehenga hoki ki te matapae, ki te whakamārama i ngā tuari raraunga ka puta i tētahi whakamātau tūponotanga;
- ka whakatau i te whaitakenga o te taurangitanga e kitea mai ana i ngā raraunga o tētahi whakamātau tūponotanga.
- ki te whakamahi hoahoa rākau hei whiriwhiri i ngā tūponotanga o ngā putanga e taea ana i tētahi horopaki tūponotanga
- ki te waihanga pūāhua tūponotanga, me te tuku pātai e hāngai ana.
Ngā taputapu hei hanga pūrere takahurihuri
Whārangi Mahi 8
Whārangi Mahi 7
Whārangi Mahi 6
Whārangi Mahi 5
Whārangi Mahi 4
Whārangi Mahi 3
Whārangi Mahi 2
Whārangi Mahi 1
He uka
He mataono tau
He pūkei kāri
| hoahoa rākau | tree diagram |
| horopaki tūponotanga | probability context |
| pāpono tūponotanga | probability event |
| pīrori | roll (a dice) |
| piu | toss (a coin) |
| pūāhua tūponotanga | probability situation |
| putanga | outcome |
| tātai tūponotanga | calculate probabililty |
- Ko te mahi tuatahi, he whakaatu rapanga ki te kauwhata rārangi, he whiriwhiri hoki i te whārite e hāngai ana ki taua kauwhata.
Ngā Tohutohu He Tauira Kōrero Mā Te Pouako Tukuna ētahi pātai tūponotanga, ka whakawhiti kōrero ai. Ko ngā pātai nei hei whakahoki mai, hei whakakorikori i te mōhio o te ākonga ki tēnei mea te tūponotanga. He aha ngā putanga e taea ana i te piunga o tētahi uka? Ka puta ko te whiore, ko te upoko rānei.
He aha te tūponotanga ka puta he whiore? Ko te haurua. E rua ngā putanga e taea ana, he ōrite te tūponotanga o tēnā me tēnā. Nō reira ko te haurua te tūponotanga ka puta he whiore.
He aha tētahi atu putanga he haurua anō te tūponotanga? He haurua anō te tūponotanga ka puta he upoko.
Mēnā ka pīrorihia tētahi mataono tau, he aha tētahi putanga he haurua te tūponotanga? He haurua te tūponotanga ka puta …
- he taukehe, nā te mea e 3 ngā taukehe o roto i ngā tau e 6 katoa
- he taurua, nā te mea e 3 ngā taurua o roto i ngā tau e 6 katoa
- he 1, he 2, he 3 rānei, nā te mea e 3 ēnei tau o roto i ngā tau e 6 katoa e taea ana.
- he tau nui ake i te 3, nā te mea e 3 ēnei tau o roto i ngā tau e 6 katoa e taea ana.
He aha ētahi pūāhua e whakamahia ai tēnei mea te tūponotanga?
Hei tauira whakautu:
Te hauora – hei tauira, ko te tūponotanga ka pāngia tētahi tangata ki te mate pukupuku. He tino rahi kē atu te tūponotanga ka pāngia te tangata kaihikareti ki te pukupuku korokoro, tērā i te tūponotanga ka pāngia te tangata kāore e kaihikareti.Tūhuratia te hoahoa rākau hei whakaatu i ngā putanga katoa e taea ana i te piunga o ētahi uka e rua. Mēnā e rua ngā piunga uka, he aha ngā putanga e taea ana?
Kotahi te upoko, kotahi te whiore.
E rua ngā whiore.
E rua ngā upoko.Me pēhea te whakaatu i ēnei putanga ki tētahi hoahoa, tūtohi rānei.
Mā te tūtohi:piunga 1 piunga 2 putanga upoko upoko uu upoko whiore uw whiore upoko wu whiore whiore ww Mā te hoahoa rākau:
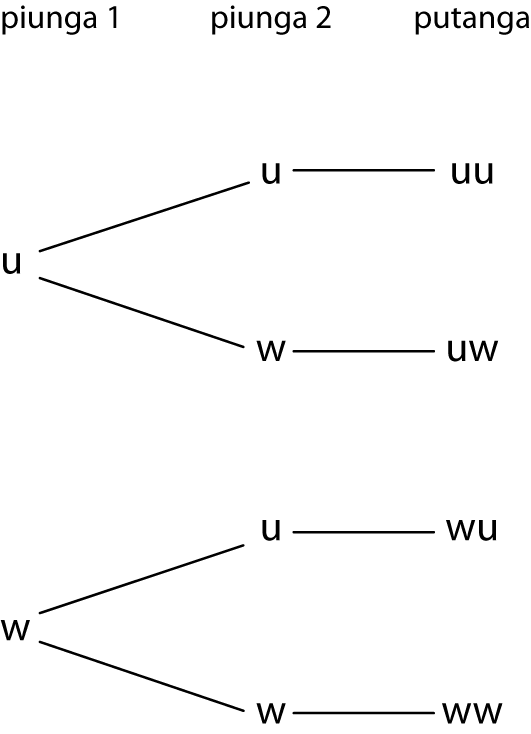
Titiro ki te hoahoa rākau, te tūtohi rānei. E whā katoa ngā putanga. He ōrite te tūponotanga o ia putanga? āe, he ōrite te tūponotanga nā te mea he ōrite te tūponotanga o te upoko me te whiore i ia piunga.
Nō reira he aha te tūponotanga ka puta ētahi upoko e rua? E 4 katoa ngā putanga, ko ngā upoko e rua tētahi o aua putanga e 4. Nō reira ko te hauwhā (1/4) te tūponotanga.
Tuhia ngā tūponotanga o ia putanga ki te hoahoa rākau, ki te tūtohi rānei.
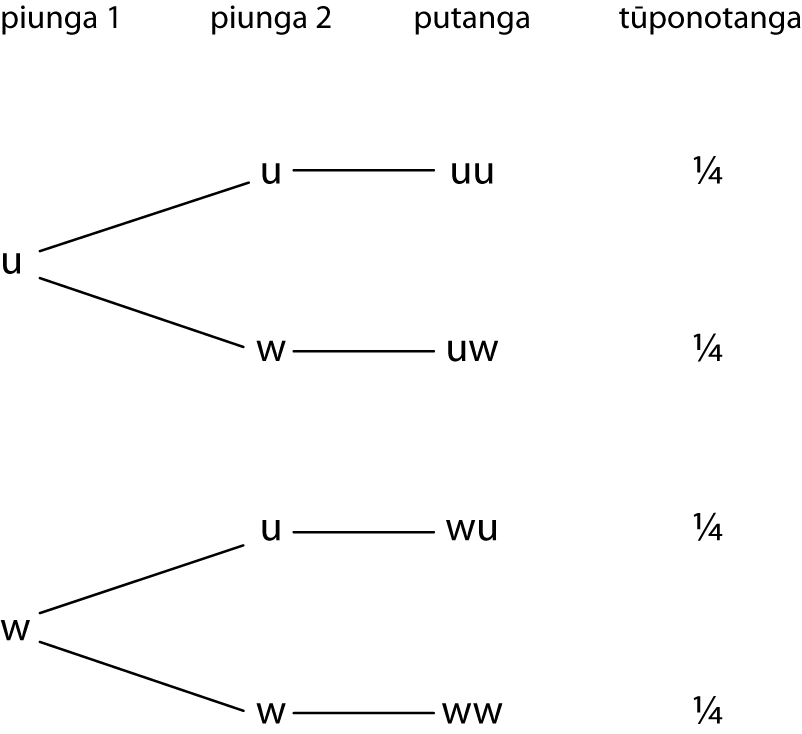
He aha te tūponotanga ka puta tētahi whiore me tētahi upoko? Ko te haurua (1/2) – he hauwhā (1/4) te tūponotanga o te ‘uw’ he hauwhā hoki te tūponotanga o te ‘wu’. Hui katoa, ko te haurua (1/2) tēnā.
Tukuna ngā ākonga ki te tūhura i te hoahoa rākau hei whakaatu i ngā putanga o ētahi piunga uka maha, me te tātai anō i ngā tūponotanga.
Whakaaturia ngā tūponotanga ki tētahi tūtohi ka kimi ai i te tauira.
He aha te tūponotanga o tētahi whiore i te piunga o tētahi uka? Ko te haurua (1/2)
He aha te tūponotanga o ētahi whiore e rua mēnā e rua ngā piunga uka? Ko te hauwhā (1/4)
Me pēhea te whakaatu i ētahi piunga uka e toru ki tētahi hoahoa rākau?
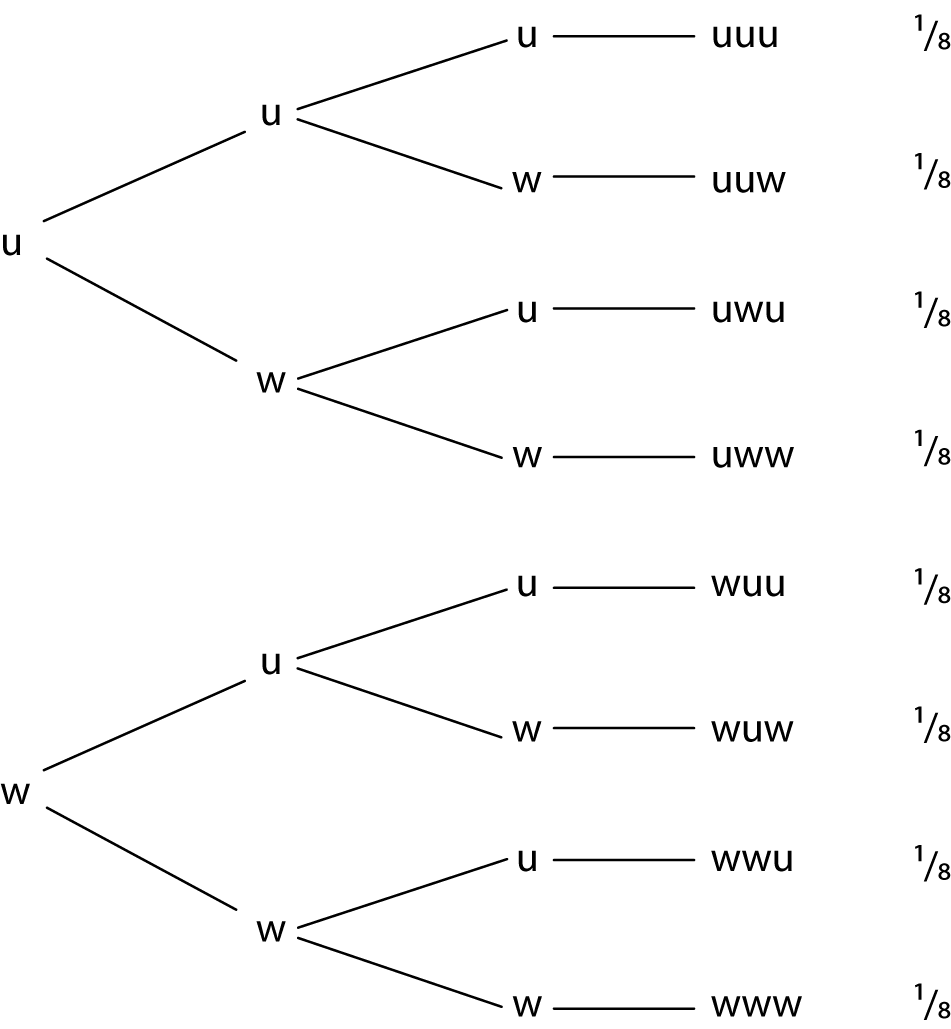
E hia katoa ngā putanga mēnā e 3 ngā piunga uka? E 8.
He aha te tūponotanga o ētahi whiore e toru? Koia te putanga kotahi o roto i ngā putanga e 8, nō reira ko te hauwaru (1/8) te tūponotanga.
Me tuhi ēnei tūponotanga ki te tūtohi:
te maha o ngā piunga te maha o ngā putanga katoa te maha o ngā whiore te tūponotanga o ngā whiore 1 2 1 ½ 2 4 2 ¼ 3 8 3 1/8 4 16 4 1/16 … He aha te tauira e kitea mai ana i te tūtohi Mēnā ka piua anō te uka, ka rearuatia te maha o ngā putanga katoa.
Ko ngā tau e kitea ana i te pou ‘te maha o ngā putanga katoa’ koia ko ngā taupū o te 2. Ka tuhia tēnei ki te tūtohi:
te maha o ngā piunga te maha o ngā putanga katoa te maha o ngā whiore te tūponotanga o ngā whiore 1 2 = 21 1 ½ = 1/21 2 4 = 22 2 ¼ = 1/22 3 8 = 23 3 1/8 = 1/23 4 16 =24 4 1/16 = 1/24 5 32 = 25 5 1/32 = 1/25 … Me pēhea te tātai i te maha o ngā putanga katoa mēnā 10 ngā piunga uka? Ko te taupū 10 o te 2, Arā, 210.
Mēnā 10 ngā piunga me pēhea te tātai i te tūponotanga ka puta ētahi whiore 10? Wehea te kotahi ki te taupū 10 o te 2. Arā, 1/210
.Me pēhea te tātai i te maha o ngā putanga katoa mēnā ko te ‘n’ te maha o ngā piunga uka? Ko te taupū ‘n’ o te 2, Arā, 2n.
Mēnā ko te ‘n’ hei tohu i te maha o ngā piunga me pēhea te tātai i te tūponotanga ko te n’ te maha o ngā whiore ka puta? Wehea te kotahi ki te taupū 10 o te 2. Arā, 1/210.
maha o ngā piunga te maha o ngā putanga katoa te maha o ngā whiore te tūponotanga o ngā whiore 1 2 = 21 1 ½ = 1/21 2 4 = 22 2 ¼ = 1/22 3 8 = 23 3 1/8 = 1/23 4 16 = 24 4 1/16 = 1/24 5 32 = 25 5 1/32 = 1/25 … n 2n n 1/2n Kia pērā anō te arataki i ngā ākonga ki te tuhi hoahoa, ki te tātai i ngā tūponotanga e hāngai ana ki te pātai nei:
He aha te tūponotanga o ētahi whiore e rua, mēnā ko te ‘n’ te maha o ngā piunga uka?
Tuhia he hoahoha rākau hei whakaatu i ētahi piunga uka e rua. He aha te tūponotanga ka puta ētahi whiore e rua? E whā katoa ngā putanga e taea ana. Kotahi o aua putanga ko ngā whiore e rua, nō reira ko te hauwhā (1/4) te tūponotanga.
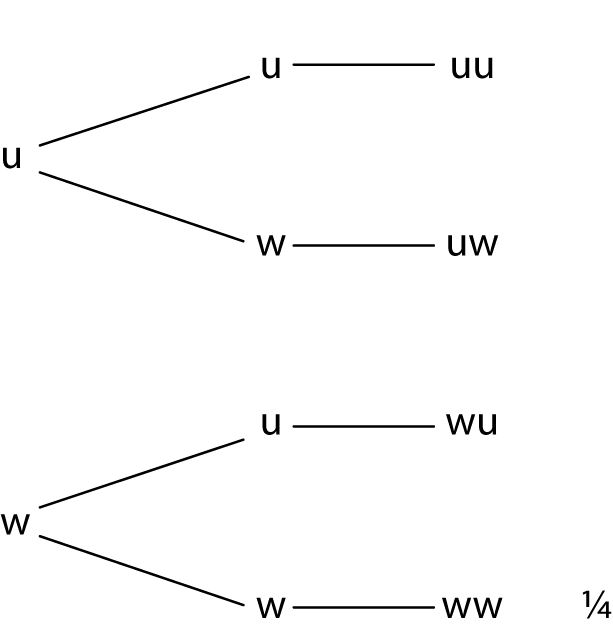
Tuhia he hoahoha rākau hei whakaatu i ētahi piunga uka e toru. He aha te tūponotanga ka puta ētahi whiore e rua? E waru katoa ngā putanga e taea ana. E toru o aua putanga ko ngā whiore e rua, nō reira ko te toru hauwau (3/8) te tūponotanga.

Tuhia he hoahoha rākau hei whakaatu i ētahi piunga uka e whā. He aha te tūponotanga ka puta ētahi whiore e rua? Tekau mā ono katoa ngā putanga e taea ana. E ono o aua putanga ko ngā whiore e rua, nō reira ko te ono hautekau mā ono (6/16) te tūponotanga.

Whakaaturia ēnei tūponotanga ki te tūtohi.
ngā piunga ngā putanga katoa ngā putanga e 2 ngā whiore te tūponotanga e 2 ngā whiore 2 4 1 ¼ 3 8 3 3/8 4 16 6 6/16 He aha te tauira e kitea mai ana i te pou ‘ngā putanga katoa’? Koia ko ngā taupū o te 2 (21, 22, 23…).
He aha te tauira e kitea mai ana i te pou ‘ngā putanga e 2 ngā whiore’. Anei tētahi: 1 + 2 = 3 + 3 = 6 + 4 = 10 …
Anei anō tētahi tauira e hono ana i te maha o ngā piunga me te maha o ngā putanga e 2 ngā whiore:
ngā piunga te hononga te maha o ngā putanga e 2 ngā whiore 2 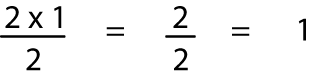
1 3 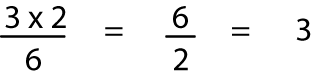
3 4 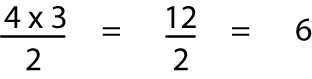
6 5 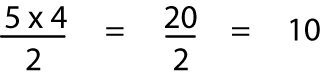
10 … Mēnā ko ‘n’ hei tohu i te maha o ngā piunga, he aha te whārite hei tātai i te maha o ngā putanga e 2 ngā whiore?
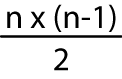
Mēnā ko ‘n’ hei tohu i te maha o ngā piunga, he aha te whārite hei tātai i te tūponotanga o ētahi whiore e 2?
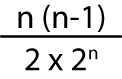
Tuhia ēnei whārite ki te tūtohi:
ngā piunga ngā putanga katoa ngā putanga e 2 ngā whiore te tūponotanga e 2 ngā whiore 2 4 1 ¼ 3 8 3 3/8 4 16 6 6/16 5 32 10 10/32 n 2n 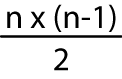
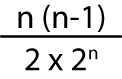
Whakamahia ngā whārite hei tātai i te tūponotanga o ētahi whiore e rua mēnā 10 ngā piunga uka.
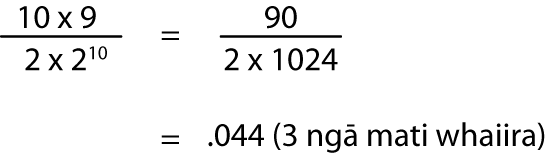
Tukuna te Whārangi Mahi 1 (PDF, 91KB)hei whakaoti mā ngā ākonga, hei mahi takirua pea. āta wānangahia ngā whakautu. - Ko te mahi tuarua, he tuku i ngā ākonga ki te mahi takitahi, takirua, takirōpū rānei ki te tātai i ngā tūponotanga kei ngā rapanga o Whārangi Mahi 2 (PDF, 90KB). He mea nui kia āta whakawhitiwhiti whakaaro mō te rautaki ka whāia, me ngā otinga ka puta.
- Ko te mahi tuawhā, he tuku i ngā ākonga ki te mahi ā-rōpū i ngā Whārangi Mahi 3 ki te 8. He rerekē te horopaki tūponotanga ki tēnā, ki tēnā o ngā whārangi mahi, engari he ōrite te mahi – he tuhi hoahoa rākau, he tātai tūponotanga, he kimi i te whārite hei whakawhānui i te tātaitanga tūponotanga.
Whārangi Mahi 3 (PDF, 110KB)
Whārangi Mahi 4 (PDF, 83KB)
Whārangi Mahi 5 (PDF, 76KB)
Whārangi Mahi 6 (PDF, 97KB)
Whārangi Mahi 7 (PDF, 104KB)
Whārangi Mahi 8 (PDF, 118KB) - Tukuna mā ngā ākonga e whakaaro, e waihanga tētahi pūāhua tūponotanga, pērā i ngā pūāhua o tēnei kōwae ako, ka tuhi ai i ētahi pātai. E pai ana te mahi takirua, me te hoatu i ngā pātai hei whakautu mā tētahi atu tokorua.
Ngā Whakautu:
Whārangi Mahi 1
- 1/8
- 4/16
- 10/32
- 20/64
- 1/8
- 4/16
- 10/32
- 20/64
- 7/8
- 15/16
- 31/32
- 63/64
Whārangi Mahi 2
- 1/8
- 3/8
- 4/8
- 4/8
- 4/8
- 0
Whārangi Mahi 3
-
a) Kia kotahi te whiore, kia kotahi rānei te upoko.
e) Kia kotahi te upoko, kotahi te whiore.
h) Kia kotahi, nui ake rānei ngā upoko. Kia kotahi, nui ake rānei ngā whiore. -
a) Kia kotahi te whiore, kia kotahi rānei te upoko.
e) He whiore te piunga tuatahi me te piunga tuarua.
h) He nui ake ngā whiore i ngā upoko. -
a) Kia kotahi te whiore, kia kotahi rānei te upoko.
e) He upoko te piunga tuatahi, te piunga tuarua me te piunga tuatoru.
h) Kia toru, nui ake rānei ngā upoko. -
a) Kia kotahi te whiore, kia kotahi rānei te upoko
Whārangi Mahi 4
- 1/9
- 2/9
- 5/9
- 6/9
- 5/9
- 4/9
-
a) He ōrite te tae o ngā rohe e rua ka tau te pūrere.
e) Kāore e tau te pūrere ki te rohe mā me te rohe whero.
h) Kāore e tau ki ētahi whero e rua. - 6/27
- 3/27
- 19/27
- 19/27
- 9/27
- 8/27
-
) Kāore e rua ngā taunga o te pūrere ki tētahi tae.
e) Kotahi te taunga o te pūrere ki te rohe whero.
h) Ka tau te pūrere ki ngā rohe katoa.
Whārangi Mahi 5
- 1/16
- 2/16
- 12/16
- 10/16
- 7/16
- 4/16
- 1/64
- 4/32
- 6/32
Whārangi Mahi 6
- 9/25
- 4/25
- 12/25
- 16/25
- 21/25
- He ōrite te tae o ngā poi e rua.
- 27/125
- 8/125
- 54/125
- 36/125
Whārangi Mahi 7
- 1/9
- 1/6
- 11/18
- 3/4
- 14/36
- 1/27
- 2/9
- 3/8
- 7/27
Whārangi Mahi 8
- 1/4
- 1/169
- 25/169
- 9/169
- 9/169
- 16/169
- 1/8
- 1/2197
- 125/2197
- 27/2197
- 64/2197