This problem solving activity has a geometry focus.

Then she realises that one is on top of the other.
She wonders how many times a day the hour hand and the minute hand on her watch are in the same position.
How many do you think?
- Find an angle greater than 360 degrees that relates to a given position.
- Solve a linear equation.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram, guess and check, use algebra).
This problem involves taking a problem about time, looking at it geometrically, and solving it algebraically. The problem is about when hands on a watch coincide. This is easily seen as a geometry problem as a diagram can be drawn to show the situation. Finding the algebraic approach may be more challenging. This requires knowing about the relative speed of the hands of a watch and the significance of angle.
Hinea’s Other Watch, Geometry, Level 6 is a similar problem.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- An analogue watch or clock
The Problem
Hinea glances at her watch. At first she sees only one hand! Then she realises that one is on top of the other. She wonders how many times a day the hour hand and the minute hand on her watch are in the same position.
How many do you think?
Teaching Sequence
- Focus the class on the clock on the wall or their own watch and pose the problem.
- Encourage the students to estimate the number of possible answers, using questions that require them to justify their guesses.
Do you know any answers already?
How many answers will there be altogether? Why?
What position will the hands be in? - While the students are working on the problem ask questions that enable them to clarify the variables involved in the time situation.
What starting strategy did you use?
What changes in this problem?
What variables do you need to consider? - Further questions that ensure students have knowledge of angles greater than 360 degrees may be needed:
About when are the angles the same?
How far has the minute hand moved?
Through what angle is this?
How can these angles be the same?
What angle is at the same position as 390 degrees? 450 degrees? - Encourage the students to write down any connections they have found in words and link these to a possible algebraic form.
- Connections need to be made between the angle and the time it represents.
How does the angle relate to the time that has passed? - Have the students share their approaches and explain the links between the speed, angles and time.
- Compare the number of answers with the predicted total from the starting discussion.
Why are there only 22 answers and not 24?
Solution
One way to do this is to turn the hands of a real clock around and count the number of times the hands overlap. Then ask how you can be sure that you have the right answer.
The minute hand goes through 360° in 1 hour. The hour hand goes through 360° in 12 hours, or 30° an hour. So the minute hand moves 12 times as quickly as her hour hand. While the hour hand is moving through an angle α, the minute hand is moving through an angle of 12α.
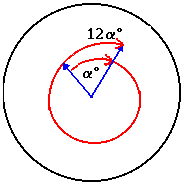
On the other hand, because they are on top of each other, 12α - 360° = α. So 11α = 360° or α = 360/11 = 32.72. This represents (32.72 / 360) x 60 minutes. This is approximately 5 minutes and 27.3 seconds.
The hands are therefore on top of each other at 0:00:00; 1:05:27; 2:10:55; 3:16:22; 4:21:49; 5:27:16; 6:32:44; 7:38:11; 8:43:38; 9:49:05; 10:54:33; and every 12 hours afterwards.
This therefore happens 22 times in a day.