Being an avid watch watcher, Hinea discovers that the hands of her watch are perpendicular at 3pm and at 9am.
She wonders how many times a day the hands of her watch are perpendicular to each other?
What answer does she come up with and why?
- Solve problems using the relationships between angles in a circle.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, guess and check, think, use algebra).
This problem involves taking a problem about time, looking at it geometrically, and solving it algebraically. The problem is about when hands on a watch are perpendicular. This is easily seen as a geometry problem as a diagram can be drawn to show the situation. Finding the algebra may be more challenging. This requires knowing about the relative speed of the hands of a watch and the significance of angle.
Hinea’s Watch's Hands, Geometry, Level 6 is a similar problem.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- An analogue watch or clock
The Problem
Being an avid watch watcher, Hinea discovers that the hands of her watch are perpendicular at 3pm and at 9am. She wonders how many times a day the hands of her watch are perpendicular to each other?
What answer does she come up with and why?
Teaching Sequence
- Focus the class on the clock on the wall or their own watch and pose the problem.
- Encourage the students to estimate the number of possible answers. Ask them to briefly explain their guesses. List their answers on the board.
- As students work on the problem ask questions such as:
What starting strategy did you use?
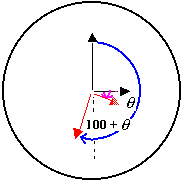
Can you describe how the hands of a clock move? In relation to each other? - If the students are having difficulty making progress with this problem encourage them to take a known time (eg 3 o’clock) and work out what the next "perpendicular" time would be. Physically moving the hands of a watch will make this easier. Next encourage the students to look at the distance moved by the two hands and see if they can describe the relationship. (Θo, 180° + Θo)
- Share solutions.
- If no-one has used the logical approach described below it would be useful to discuss this with the students.
Solution
In the first instance, this problem can be attempted by trial and error using a real watch.
Suppose the hour hand moves Θo between two consecutive perpendicular occasions. Then the minute hand moves 180° + Θo.
The time taken is 
hours (the hour hand moves 1/12 x 360° = 30° per hour). But the minute hand moves 12 times as fast as the hour hand (the minute hand goes around 12 times to the hour hands once). So the time taken to move 180° + q ° is 
. Hence .gif){kind=small}
= .gif)
. This gives q = 
and the time between two perpendiculars is 180/11 x 1/30 hours. Hence the number of perpendiculars in 24 hours is 24 / (180/360) = 44.
Note that there is a "logical" approach to this problem. Between one hour and the next, the hands of a clock have to be perpendicular twice. This seems to suggest that this would produce 48 (2 x 24) perpendicular events a day. However, at 3 o’clock the hands are perpendicular on the hour. So these occurrences take place between 2 and 3 o’clock as well as between 3 and 4 o’clock. So we lose one perpendicular event as a result. The same thing happens at 9 o'clock. Hence we need to subtract 4 perpendiculars from the original guess of 48 (one for each of 3am, 9am, 3pm and 9pm). So there are 44 perpendiculars in a day. (The answer to Hinea’s Watch's Hands problem is 22. You might consider with your students whether or not it is a coincidence that 44 = 2 x 22?)