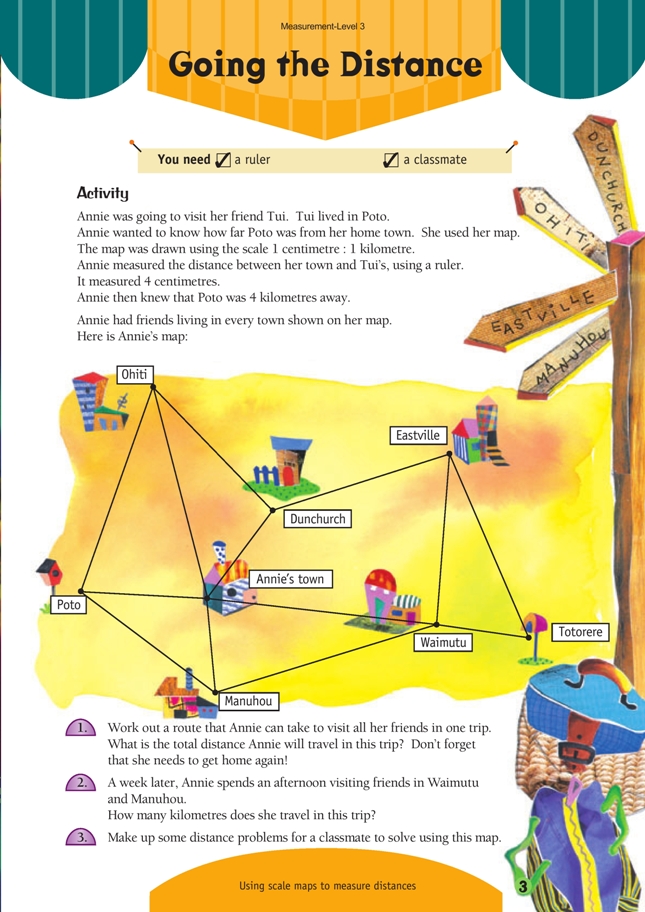
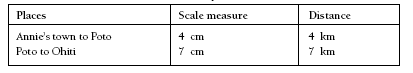This is a level 3 measurement and geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (230 KB)
use scale maps to measure distances
FIO, Level 3, Measurement, Going the Distance, page 3
classmate
This activity involves estimating and measuring length in centimetres. The major focus is to calculate distances using a scale drawing.
This is an ideal activity to encourage estimation. Initially, you could ask students to estimate the distance in centimetres between two towns. Have them make a chart to help them convert this to the actual distance in kilometres, for example:
Those who are confident with the idea of scale drawing could estimate the distance in kilometres straight away and explain their answer.
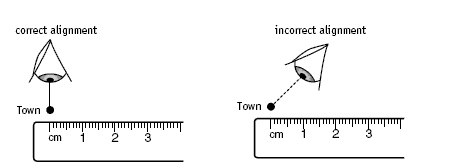
Encourage accuracy with the use of the ruler by insisting that students look directly down on the town they are measuring as they align their ruler and read the measure. Make sure that they start at the beginning of the scale on the ruler and not at the 1 centimetre mark.
Change the scale to provide some additional practice with calculating a scale distance, for example,
1 centimetre : 2 kilometres
1 centimetre : 4 kilometres
1 centimetre : 8 kilometres
1 centimetre : 16 kilometres
This could be extended to:
1 centimetre : 2.5 kilometres
1 centimetre : 7.25 kilometres
Make a point of focusing students’ attention on how the scale is written using the colon and how to interpret the instruction “The scale is 1 centimetre to 4 kilometres”. Help them to see that this is the same instruction as saying “1 centimetre on the drawing shows 4 kilometres of actual distance”.
Ensure that students who make up some distance problems, as in question 3, are responsible for checking the answers to their problems and are prepared to explain their answers if necessary. This will encourage them to make up sensible problems and help reinforce their understanding of scale measurement.
Answers to Activity
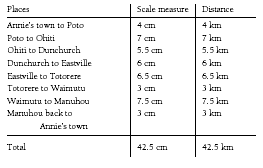
1. There are many possible routes. Some routes will have equal distances while others will be different. Here is an example of a route with the distances measured. The scale is 1 cm : 1 km.
2. 18 km
3. Answers will vary.