This is a level 5 number activity from the Figure It Out series. It relates to Stage 8 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (591 KB)
investigate fractions and proportions
This activity about the changing value of gold krugerrands is similar to another relatively well-known problem involving workers’ wages being cut by 10 percent in a time of company hardship but then increased by 10 percent a year later when the company’s fortunes improved. Were the workers now back to their previous
level of wages? The answer is no! Imagine, to take a nice round figure, that the workers were earning $100 per week. If their wages were reduced by 10 percent (that is, by one-tenth), they would be earning $90 per week. Increasing them again by 10 percent means that 10 percent or one-tenth of 90 would be added. The
workers would now be earning $99 per week, not their original $100 per week.
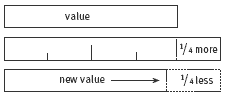
The same is true of the value of the krugerrands. Let’s say the krugerrand was worth $8 at the beginning of the previous year and that its value had increased by half or 50 percent. That meant that it would then be worth $12. Now, with the drop in value again, that is, to a level that is just half of last year’s value, each krugerrand is now worth just $6. So, over the 2 years, krugerrands have dropped in value from $8 to $6. This drop of $2 on the original value means that they have lost 25 percent or one-quarter of their value. Hence, they are now worth only three-quarters or 75 percent of their value at the beginning of the previous year (6/8is the same as 3/4). The diagram on the student page shows visually how and why this drop in overall value occurred.
When the students come to question 2, they will probably follow similar steps to those that Leyton used in his diagram. This time, however, they will need to divide their diagram into four equal lengths. A convenient length to begin with would be 16 centimetres. When this is increased by one-quarter (that is, 4 centimetres),
it becomes 20 centimetres. When this is then decreased by one-quarter (that is, 5 centimetres), it reduces to 15 centimetres.
Now would be a good stage to help the students to see what is happening more generally. With first an increase and then a decrease of half, the result is a loss of one-quarter of the original value. When there is an increase and then a decrease of one-quarter, the result is a loss of one-sixteenth of the value. Thus, a pattern begins to emerge:
1/2 x 1/2 = 1/4
1/4 x 1/4 = 1/16
That is, the final decrease is equal to the original increase/decrease amount squared.
These problems can also be approached directly using fractions. If we increase something by one-half, we are effectively multiplying it by 3/2. If we then reduce it by one-half, we are effectively multiplying the result by 1/2, which is equivalent to calculating 3/2 x 1/2, which is 3/4. That is, we now have three-quarters of our
original quantity. Similarly, with an increase/decrease of one-quarter, we have 5/4 x 3/4 = 15/16.
The same approach can be used for question 3. For example, an increase of one-third followed by a decrease of one-third is equivalent to calculating 4/3 x 2/3 = 8/9.
Encourage the students to find out (using diagrams and calculation) whether or not the order in which a quantity is increased and decreased is important. For example, an increase of one-third followed by a decrease of one-third will give the same result as the decrease followed by the increase (though the intermediate quantity will clearly be different).
By looking at results such as those above, the students may notice that the numerator of the fraction that results is always one less than the denominator. If they can couple that with the fact that the denominator is found by squaring the increase/decrease amount, then they may be able to arrive at the formula given in the Answers.
In question 4b, the students need to convert the 1 percent to the fraction 1/100. They can then apply the rule that they have discovered in a to work out that the “something” has decreased in value by 1/10 000 (1/100 x 1/100) and is now worth 9 999/10 000 of the original value.
Answers to Activity
1. a. Yes.
b. They have decreased by 1/4 and are now worth only 3/4 of their value of 2 years ago.
2. A possible diagram is:
3. a. 8/9 of the original value
b. 24/25 of the original value
c. 35/36 of the original value
4. a. The general rule for a fractional increase followed
by a decrease of 1/n is (n2 – 1)/ n2
b. 9 999/10 000