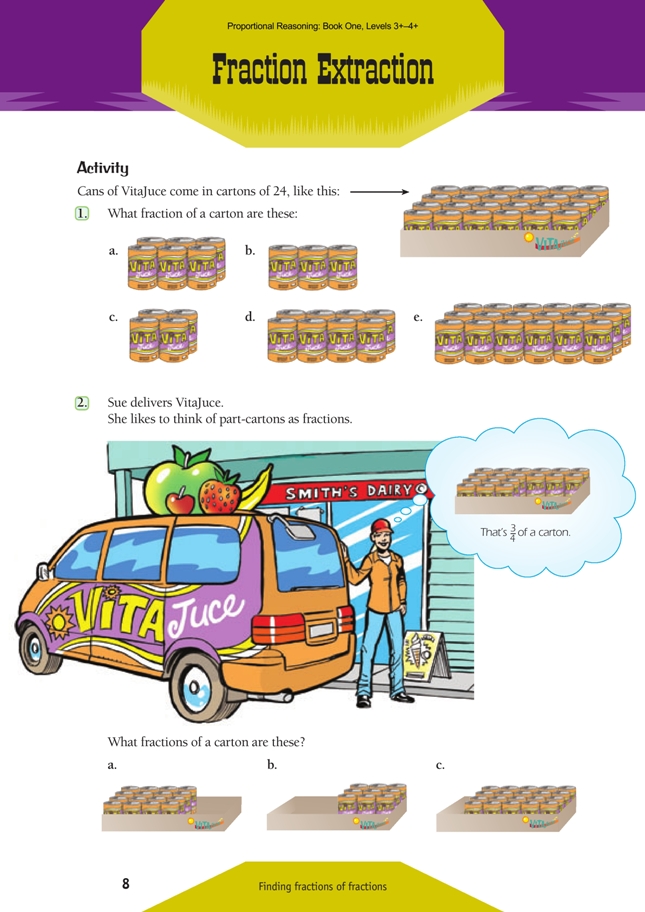
This is a level 5 number activity from the Figure It Out series. It relates to Stage 8 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (923 KB)
find fractions of fractions
Number Framework Links
Use this activity to:
• encourage the transition from advanced multiplicative strategies (stage 7) to advanced proportional strategies (stage 8)
• develop confidence in students who are beginning to use advanced proportional strategies (stage 8).
This activity creates meaning for the concept “division of a fraction by a fraction”.
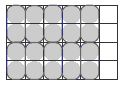
The carton uses a set (24 cans) as a unit or whole. Students should understand that this can be represented mathematically by the equation: 24/24 = 1.
The illustrations on the page provide good support for an introductory discussion leading into this activity. If further support from materials is needed, use counters to represent the cans.
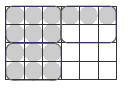
Use question 1 to establish that your students understand fractions of a set and can express them as equivalent fractions in their simplest form.
Encourage your students to make statements such as “A 6-pack is 6 out of 24 so it is a quarter of a carton.” They should record this as 6/24 = 1/4. You could also ask them to record their statements as ratios, like this: 6:24 = 1:4.
Ask confident students to explain how to simplify the fraction using number properties: “The only way we can divide a number without changing its value is to divide it by 1. So to siplify the fraction we need to divide it by a suitable equivalent of 1. Of all the possiblilities, which should we try?” 6/6 is the fraction they need. Students can record the division operation in this way: 6/24 ÷ 6/6 = 1/4.
Question 2 gives the students further practice at finding fractions of a whole and expressing them in their simplest forms.
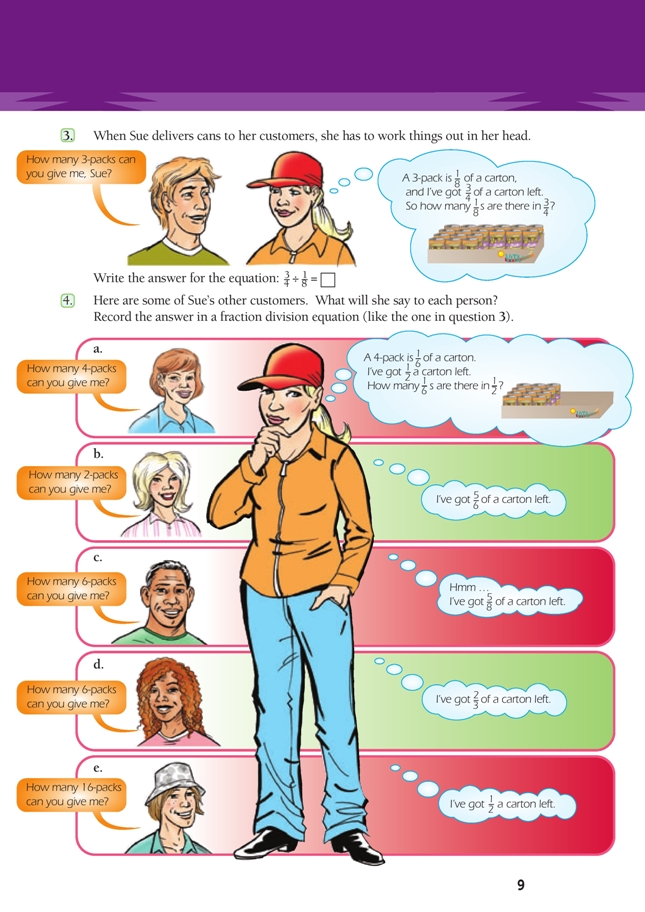
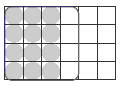
Question 3 introduces the idea that one fraction can be divided by another. The speech and thought bubbles give the students the clues they need to solve each problem. Guide them through the problem using numbers of cans: “How many cans are in the carton?” “How many 3-packs are in the carton?” “Why is the question ‘How many 3-packs are there in 3/4 of a carton?’ the same as ‘How many 1/8 s are in the carton?’ ”
It is vital that students connect these “How many … in?” questions so that when they read division equations, they can interpret them in ways that are meaningful to them. 3/4 ÷ 1/8 = can be read as “ 3/4 divided by 1/8 equals what?” but it means “How many 1/8 s are there in 3/4 ?”
Another approach is to ask “Can we use equivalent fractions to make it easier to see the answer?” A response might be “If we change 3/4 into 6/8, we can see that there are 6 one-eighths in six-eighths. So 6/8 ÷ 1/8 = 6.”
Questions 4c and 4d increase the challenge because both solutions are mixed numbers. If students reinterpret question 4c as “How many 2/8s are in 5/8?”, they will find it much easier to make sense of the problem.
Show your students how to set the problem down mathematically. Rewrite 5/8 ÷ 1/4 in the form 5/8 ÷ 2/8, making use of an equivalent fraction for 1/4. Now divide one numerator by the other (5 ÷ 2 = 2 1/2) and one denominator by the other (8 ÷ 8 = 1). The result is 2 1/2 ÷ 1 = 2 1/2 . This makes meaningful use of number properties to solve a division-by-a-fraction problem instead of the traditional “rule”: to divide by a fraction, multiply by its reciprocal (or, invert and multiply).
Question 4e can easily be misinterpreted. Put students into mixed-ability problem-solving groups with not more than four members and have them find and justify an equation that matches the problem. The question is “How many two-thirds cartons can be made from one half carton?” Expressed slightly differently, this is “How much of 2/3 is in 1/2?” The appropriate equation is 1/2 ÷ 2/3 =. If some students can’t see this, they should go back to any “goes into” equation that
they do understand and see how this one follows the same pattern.
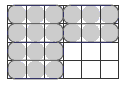
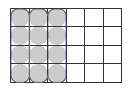
Using equivalent fractions, 1/2 ÷ 2/3 =can be rewritten in the form 3/6 ÷ 4/6 =. Dividing one numerator by the other gives . Dividing one denominator by the other gives 1. 3/4 ÷ 1 = 3/4. This shows that a half carton is the same as three-quarters of two-thirds of a carton! Match this statement to a diagram of two thirds of a carton so that students can visualise it (as in the Answers).
Answers to Activity
1. a. 1/4 b. 1/8 c. 1/6
d. 1/3 e. 3/4
2. a. 2/3 b. 3/8 c. 5/6
3. 3/4 ÷1/8 = 6. Sue can give them six 3-packs.
4. a. 1/2 ÷ 1/6 = 3. Sue can give them three 4-packs.
b. 5/6 ÷ 1/12 = 10. Sue can give them ten 2-packs.
c. 5/8 ÷ 1/4 = 2 1/2. Sue can give them two and a half 6-packs.
d. 2/3 ÷ 1/4 = 2 2/3. Sue can give them two and two-thirds 6-packs.
e. 1/2 ÷ 2/3 = 3/4. Sue can give them three-quarters of a 16-pack.