The purpose of this unit is to support students to represent number problems as equations, and to strategically choose the best operation to solve problems in context.
- Understand that an unknown amount or number can be represented with a symbol: a question mark, a shape or a letter.
- Recognise that to find the value of the missing number, you have to ‘undo’ what has been done to it.
- Write word problems of real-life situations and express these with equations that include an unknown.
- Recognise that an equation is balanced around the equals symbol.
- Formally solve equations, which include unknowns, using inverse operations where needed.
- Estimate values for unknown amounts and explain reasoning.
- Recognise that the calculator is a useful but ‘fallible’ tool (i.e. capable of making mistakes) whilst recognising that the correct choice of operation is critical.
Linear equations are equations which, when plotted on a graph, create a straight line.
In these types of equations, an unknown amount or number can be represented with a symbol (e.g. the letter “x”). The process of finding these unknown values is foundational knowledge for a good understanding of algebra at Level 5 of the New Zealand Curriculum. Key to this knowledge is the understanding that the equals sign communicates equivalence between two amounts. Often, students perceive the equals sign as meaning “the answer is”. It is important to build on this understanding using written equations which show that the amount on the left hand side of the equals sign is the same as the amount on the right hand side. Single-step finding of unknowns can be classified in this helpful way:
| Operation | Result unknown | Change unknown | Start unknown |
| Addition | 4 + 6 = [ ] | 4 + [ ] = 10 | [ ] + 6 = 10 |
| Subtraction | 10 - 6 = [ ] | 10 - [ ] = 6 | [ ] - 6 = 4 |
| Multiplication | 3 × 5 = [ ] | [ ] × 5 = 15 | 3 × [ ] = 15 |
| Division | 15 ÷ 3 = [ ] | 15 ÷ [ ] = 5 | [ ] ÷ 3 = 5 |
To solve these equations, knowledge of inverse operations is needed. Addition and subtraction are inverse operations, and so are multiplication and division. Students may find it helpful, in this context, to think of inverse operations as “cancelling” each other out.
To engage students in the context of linear equations, it is important they have opportunities to solve problems that reflect relevant real-life situations.
For example, 4 + [ ] = 10 might be framed as “Sid has 4 apples. He picks some more apples and now he has 10 apples. How many apples has he picked?” The problem could be solved as subtraction, 10 - [ ] = 4, but the context is one of joining sets of apples.
Varying the location of the unknown substantially changes the difficulty of the problem, assuming the numbers are similar. To scaffold your students in their understanding of this, you might refer to “change” unknown, “result” unknown, and “start” unknown problems. Result unknown is significantly easier than change unknown and start unknown. Generally students are more familiar with result unknown so it is important to ensure they are meeting many examples of the latter two.
Change unknown problems, such Sid’s original apple picking problem, involve considering the possibilities for change. They can be expressed as a + ? = b
"Result" unknown problems involve using given values to find a total amount. They can be expressed as a + b = ? .
"Start" unknown problems require inverse thinking since there is no beginning state. For example, “Sid has some apples. He picks six apples and now he has 10 apples. How many apples did Sid have to start with?” This "start" unknown problem changes the operation to subtraction. This can be represented as ? = 10 - 6. This involves reconceptualising the role of the whole and parts.
To support knowledge of these different types of equations, students should experience opportunities for estimating values and explaining their reasoning. Calculators and materials (e.g. laminated number lines, counters) may be a useful tool to use within this stage. When using a calculator, it is important to emphasise that the use of correct operations is essential.
For some students, algebra may be a source of anxiety. However, algebra should be celebrated as an important means of communicating mathematical statements. To support students in their learning of the concepts in this unit, you may adapt the learning opportunities provided, by removing or adding support for students and by varying the task requirements. Students need to focus on the decision-making process of which operation/s to use. While the development of calculation strategies can be facilitated through solving the problems, that is not the primary purpose. Ways to support students include:
- providing physical materials, including toy money, so that students can act out problems, connect to the operations they choose, and justify their solutions
- preparing questions that focus on the use of whole numbers, and extending students with the use of decimal numbers
- providing schematic diagrams of the problem situations to support students to recognise the structure of a problem, e.g. joining, separating, finding difference, combining equal sets, equal sharing, and measurement
- using important mathematical vocabulary to discuss situations, in particular words for equality (sameness or balance), inverse (doing and undoing), join, separate, and difference (for addition and subtraction problems), equals sets, sharing, measuring (for multiplication and division)
- giving everyday meaning to symbols, such as ‘of’ for multiplication (x), equally shared for partitive division, and ‘measured with’ for quotative division
- encouraging tuakana-teina by allowing students to collaborate, share, and justify their ideas in small groups
- altering the complexity of problems in three main ways; number complexity, location of the unknown (result unknown easier than change and start unknown); and support from materials/diagrams (degree of abstraction)
- permitting access to calculators, where appropriate, to ease the demands of calculation in favour of decision making about operations to use, and ways to record the operations as equations.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. A menu from a school cafeteria, or tuck shop, and a fruit and vegetable shop provide the contexts of the unit. You may need to show students a video clip of lunch schemes in larger schools or overseas to help them appreciate the usefulness of the context. If the food-based contexts are culturally inappropriate to your students, change the items to those that match the everyday situations students regularly encounter, e.g. prices at the school fair, the cost of new equipment for the sports-shed, the cost of food for a community hui (meeting), the cost of new native plants for a school garden. When utilising money as a context for learning, it is also important to recognise that individuals have different experiences of, and perspectives towards money.
Te reo Māori vocabulary terms such as tāpiri (add, addition), tango (subtract, subtraction), huatango (difference), whakarea (multiply), whakawehe (divide, division) and ōrite (equal, same) could be introduced in this unit and used throughout other mathematical learning.
- Plastic cubes, counters, or other singular objects
- Toy money
- Calculators
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- PowerPoint 1
Session 1
In this session students use the clues provided to find out the prices of items on a menu. The clues involve applying addition and subtraction with unknowns.
- Show your students Copymaster 1, ideally on an interactive whiteboard or other large screen.
Here is the menu from the Cafeteria at Kiwi School.
What is a cafeteria?
What is meant by daily specials on this menu? (A cycle of options available on days of the week)
Explain what is meant by Regular Daily Items? (Items that are always on sale, no matter the day of the week)
Ensure that students know what is meant by snacks and drinks.
- Invite students to imagine they are at Kiwi School and need to order their lunch for today.
Give them some time to decide on their preferences, using the provided menu, and to record those preferences. During this, links could be made to the Food and Nutrition Area of the Health and Physical Education section in the New Zealand Curriculum.
- Share some choices with the whole class.
How much will you pay for your lunch today?
Students may notice that the prices are not visible.
Luckily we have a set of clues to help us work the prices. Before we start, can someone clarify what a combo is.
Ensure that students recognise "combo" is short for combination.
What is a combination?
- Discuss how food sellers use combos to entice customers to buy several items at a discounted price. At this stage, you could make links to food combos that students order in their local community (e.g. two pieces of fish and one scoop of chips). You might discuss why students choose to order combos rather than separate items (e.g. convenience, price)
- Use PowerPoint 1 to work through the clues. Ensure that students have access to the list of food items (Copymaster 1) during this discussion. Discuss the following points:
- Clue One: If the cost of two choices is $5.00 what might one choice and three choices cost?
What are the possible options for one choice and three choices?
How could we organise those possibilities?
Ask students to write some possibilities on their copy of the menu, e.g. $1.00 and $2.00, $2.00 and $4.00, $3.00 and $6.00, etc.
Which possibilities are unlikely?
One choice must be cheaper than two choices otherwise people would not buy one choice.
Must the prices be whole dollars? What does that mean for the possibilities?
Since there are a huge range of possibilities it might be better to write a rule, like 2 x, to show the relationship. Watch to see how your students record their rule. - Clue Two: Does that tell you the cost of one daily item? How?
If two daily items cost $5.00 then each item must cost $2.50. - Clue Three: How can we work out the cost of one snack and one beverage?
$2.50 - $1.00 = $1.50 is the cost of one snack and $2.50 – $0.50 = $2.00 is the cost of one beverage. - Clue Four: How can we use this clue to work out the cost of the daily specials?
3 x $2.00 = $6:00 so the cost of three choices equals $6.00
What is the cost of one choice?
Record [ ] x 2 = $6.00 so [ ] = ? ($3.00 - cost of one choice)
- Clue One: If the cost of two choices is $5.00 what might one choice and three choices cost?
- The other slides on PowerPoint 1 give clues to work out the cost of combos. Let your students work through the clues in pairs. You may choose to pair up more knowledgeable students with less knowledgeable to encourage tuakana-teina and collaboration. Look to see that students:
- Use the menu to organise the data as they work through clues.
- Calculate accurately and fluently with the money amounts.
- Accept when unknowns must be reasoned with, even when the value is unknown.
- After a suitable time, bring the class together to share the students’ solutions. Ask students to justify how they got their answers. You may support students by working through the answers to each question as a group. Materials (e.g. laminated or digital number lines) could also be used to model working.
Combo 1: $6.50 Combo 2: $7.50 Combo 3: $8.00 Combo 4: $3.00
Remind them to order the lunch they chose and calculate the cost of it.
Was it cheaper for you to order a Combo?
- Discuss the situations in the task when the actual values were not known.
For example, Combo 2 and Combo 4 cost a total of $10.50.
How did you record that clue?
Students might have drawn arrows connecting the Combos on the menu, or have other strategies.
Record: C2 + C4 = 10.5
What might that equation mean?
I could record the same relationship as ○ + □ = 10.5
Which way do you think is better?
The key point is that the meaning of the symbols needs to be clear. It is good practice mathematically to define what both symbols represent. It may be useful to decide on specific symbols to use, as a group.
How might you record the clues, “One snack costs $1.00 less than one daily item, and one beverage costs 50 cents less than one daily item”?
Students might invent notation like; s = d - 1 and b = d – 0.5 or use ‘empty’ shapes instead of the letters.
Session Two
In this session students explore "change" and "start" unknown addition and subtraction problems. They should record their solution strategies as equations with specific unknowns, and should recognise when either addition or subtraction can be used to solve a problem.
- The staff at Kiwi School Cafeteria think that some prices need to go up because the cost of the food has increased. They also think that some prices should go down as students and teachers are not buying some items.
- Here are some examples:
The new price of regular daily items is $3.40.
What was the old price?
What is the price increase?
Let students solve the problem in pairs before sharing their strategies as a whole class.
Use words, equations, and empty number lines to record their strategies.
By change unknown addition:
“$2.50 add what equals $3.40?”
2.50 + [ ] = 3.40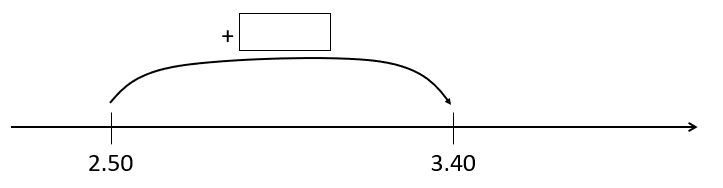
Students are likely to find the change in incremental jumps, like this, with $3.00 used as a benchmark.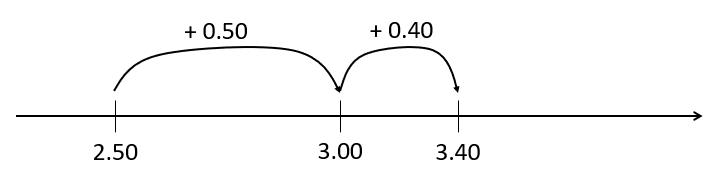
If no students use subtraction to solve the problem, you might model a solution as:
“$3.40 subtract $2.50 equals what?”
3.40 - 2.50 = [ ]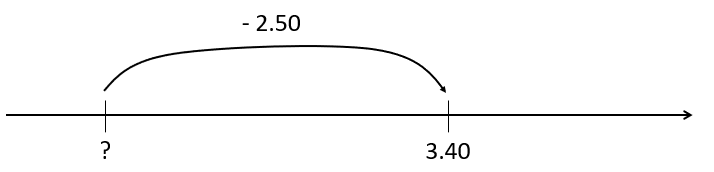
Which strategy is the most efficient for the problem? (Addition is much easier).
Encourage students to justify why they think one strategy is more efficient.
- Pose price drop problems like:
The new price of Combo 2 is $6.80.
What was the old price?
What is the price decrease?
This problem is a change unknown subtraction problem that can be represented as:
“$7.50 subtract what equals $6.80”
7.50 - [ ] = 6.80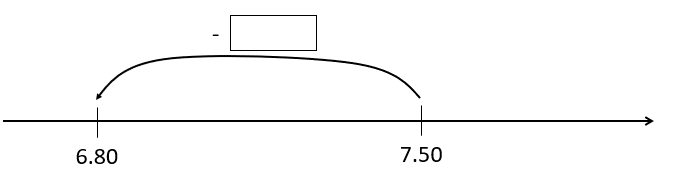
Students are likely to use incremental jumps to find the missing number (subtrahend).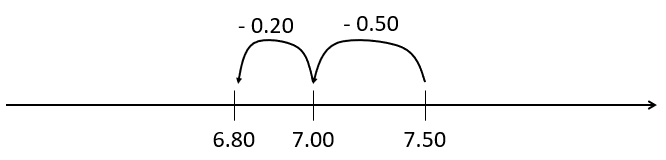
Could the problem be solved using addition?
The use of change unknown addition looks like this:
“$6.80 add what equals $7.50?”
6.80 + [ ] = 7.50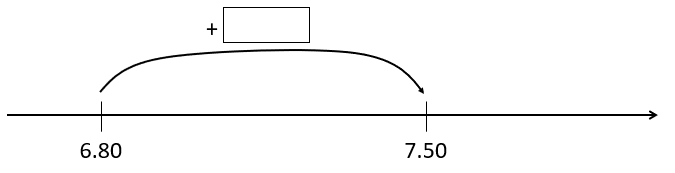
- Provide your students with Copymaster 2 that contains a range of problems for them to represent and solve. You could supplement these with problems that reflect the context of your classroom. For example, links could be made to food being sold at the Hokitika Wild Foods Festival, or the Moana Nui Festival. More knowledgeable students could also design their own questions to present to the class.
- After an appropriate time, gather the class to share solutions.
Highlight the use of equations and empty number lines as recording strategies.
Answers to Copymaster questions:
- 1.50 - [ ] = 0.90 or 0.90 + [ ] = 1.50. The price has decreased by $0.60.
- 2.00 - [ ] = 1.30 or 1.30 + [ ] = 2.00. The price has decreased by $0.70.
- Answers will vary but 0.80 + 1.40 = 2.20 so $2.00 is a good new price for Combo 4.
- The price increases are one choice ($0.70), two choices ($1.40), and three choices ($2.10). There is a consistent increase of $0.70 per choice.
- The old price of the combo had a discount of $1.50.
Adding the new prices and applying that discount gives:
3.70 + 3.40 + 0.90 + 1.30 – 1.50 = $7.80
Other answers are possible. - The equation is [ ] - 0.80 = 2.50 or 2.50 + 0.80 = [ ]. The previous price for one pie was $3.30.
Session Three
In this session students represent change and start unknown problems with multiplication and division. They do so in the context of the Kiwi School Cafeteria used in the previous two lessons. The focus in this session is more on making sensible decisions about the operations to perform than on strategies for calculation. ‘Unfriendly’ amounts are used for the prices and students are required to choose appropriate operations to solve the problems.
- Begin with the Cafeteria Manager’s problem. Give your students Copymaster 3 which has the menu with updated prices.
The Manager sees that Room 7 ordered $17.00 worth of Regular Daily item 1, the stuffed potato. The class monitor has not written how many potatoes are ordered.
How can the manager work out how many potatoes to send to Room 7?
What information do we need to solve this problem? (The price of Regular Daily Items is $3.40 each)
What operation do we need to perform?
Students might realise that they need to answer “$3.40 multiplied by what number equals $17.00?”
How can this problem be written as an equation? ([ ] x 3.40 = 17.00)
Is there another operation that might be used?
What would the equation for that operation be? (17 ÷ [ ] = 3.40 ($17.00 shared into how many equal amounts equals $3.40?) or 17.00 ÷ 3.40 = [ ]($17.00 measured in amounts of $3.40 gives how many amounts?))
The second option for division gives a direct answer of five items. Let students use a calculator to find their answer then use five as the unknown in the other two equations.
5 x 3.40 = 17.00 (The calculator will not show whole number amounts with a decimal point)
17 ÷ 5 = 3.40
- Point out that the manager faced even harder problems when monitors did not record the orders correctly.
One day a single order came in from Room 2. The total amount was $25.90 and the form said “7x”. The manager knew that each student had ordered the same kind of item but what was it?
What does 7x mean on the order? (Seven, of the same item, are ordered)
What equations could we use to record the problem?
How could the manager work out what kind of item was ordered?
7 x [ ] = 25.90 25.90 ÷ 7 = [ ]
Use the equations to find out what kind of items were ordered.
Students might use the multiplication equation but that involves a trial and error process until the correct amount is found, e.g. 7 x 4.00 = 28.00, 7 x 3.00 = 21.00, etc. The division equation gives a direct answer. Substitute the answer back into the unknown in the multiplication equation to verify that both equations give the same result for the unknown, $3.70.
What type of item is this order for? (One Choice Daily Specials)
- Some problems for the manager are when the total cost is missing.
For example:
Room 12 sends in an order for 9 students who want to buy Combo 2 at $7.80 each.
The manager checks to see that the money inside the class envelope is correct.
How much money should there be?
Students will probably recognise that this is a result unknown multiplication problem.
What equations can you write to represent this problem?
9 x 7.80 = [ ]
How could we write the same problem as division?
[ ] ÷ 7.80 = 9 or [ ] ÷ 9 = 7.80
Discuss what each equation means, e.g. “The unknown total amount shared among the nine orders equals $7.80 for each order?”
Which way to record the problem is the most sensible?
Clearly the multiplication gives a direct answer, of $70.20.
- Give students Copymaster 4 to share among a group of three students.
- Students cut up the cards and put the six order cards in separate places.
- Students assign the equation to the order card that matches it.
- Students choose six different cards and record the problem that the equation solves, e.g. The order for Room 3 totals $115.20. Each pairing of Daily Specials items costs $6.40. How many two-special items are ordered?
- Discuss the responses to part c.
Can students explain the use of numbers and operation in the problem they write?
In particular, observe that they understand the difference between sharing and measurement division.
Session Four
In this session students explore situations in which more than one operation is involved, and they learn to discriminate between additive and multiplicative situations. To allow for more flexibility the context is changed from a canteen to a fruit and vegetable store. At this stage, the context could be changed to further reflect the cultural diversity of your students. For example, students could remake Copymaster 5 with foods of their choice, and use the provided questions to plan a menu for a shared celebration involving kai. An investigation into traditional hākari (feasts) could ignite interest in this learning. In te ao Māori, different times of the year (e.g. the kūmara harvest in March) were celebrated with different hākari. To extend more knowledgeable students, hardcopy (or online) supermarket pamphlets could be used to provide more complex numbers for the different food items.
- Give students a copy of Copymaster 5 to share in pairs. Pose this problem:
Imagine you go to Pip’s Fruit and Vege Shop with $20.00 in total to spend. You must buy at least two different foods.
What will you buy?
How will you calculate the total cost?
What change will you get?
- Allow the pairs sufficient time to create an answer. You might provide a calculator for some students as the emphasis is on choice of operation rather than calculation strategies. For other students, the task provides an excellent opportunity for the mental calculation they are likely to use in real life.
- Share students’ answers in this way:
Record the operations you performed to get your total cost. We will try to figure out what you bought.
For example, a pair of students might record 1.5 x 2.79 + 3 x 1.99 + 2.4 x 3.70 = $19.04.
Students might work out that they bought 1.5kg of bananas, 3 avocados, and 2.4 kg of apples.
- After a period of sharing, pose more demanding problems that involve several operations. Here are some possibilities with answers:
Tim and Iti spent a total of $17.50.
They bought 3.5 kg of mandarins and an amount of onions.
How many kilograms of onions did they buy?
An equation might look like this:
3.5 x 2.65 + [ ] x 2.75 = 17.50
How can we work out the amount that Tim and Iti spent on onions? (Subtract 17.50 – (3.5 x 2.65) = 8.23 (rounded))
What operation will tell us how many kilograms of onions they bought? (8.3 ÷ 2.75 = 2.99)
Tim and Iti bought about 3kg of onions.
- Petra and Josefa bought 2.3 kg of beans and 5 kg of potatoes. How much more did the beans cost than the potatoes?
An equation might look like this:
2.3 x 4.50 - 5 x 1.35 = [ ]
Notice that a difference is found by subtraction or adding on.
5 x 1.35 + [ ] = 2.3 x 4.50
In this case subtraction gives direct access to the difference of $3.60.
- Lana and Tyrese bought 4 kilograms of fruit.
They bought 2 kilograms each of two different fruit. The total cost was $13.10.
What fruit did they buy?
An equation might look like this:
2 x [ ] + 2 x ( ) = 13.10
How can we find the total cost of 1 kilogram of each fruit? (divide by two)
[ ] + ( ) = 6.55
What two fruit prices match $6.55 per kilogram?
Students might realise that one price will need to have 5 in the hundredths place while the other must have 0 in the hundredths place. Only kiwifruit and plums will work.
- Ask your students to pose their own multi-operation problems for another pair to solve. The problems they create might be collected into a book of problems about Pip’s Shop.
- Roam as students create their problems.
How adventurous are they in combining the operations? (Do they stay in safe territory with addition and subtraction, or multiplication and division?)
Do they provide a solution to their problem showing the steps as equations?
- After students spend an appropriate time creating problems change the focus to which operation to use. Copymaster 6 has several problems designed to see if students can make appropriate decisions about the operation/s to use.
- Allow students sufficient time to solve the problems in pairs then discuss the solutions as a class. Drawing diagrams and acting out the problems may support some students to develop solutions. Below are notes on each problem:
- The difference in price is constant thought students are not told what that amount is. In February kiwifruit cost 12 ÷ 3 = $4 per kilogram while apples cost 9 ÷ 3 = $3 per kilogram. The price difference is always $1 per kilogram.
In May apples cost $15 ÷ 3 = $5 per kilogram. Therefore, the price of kiwifruit is $5 + $1 = $6 per kilogram. - The basket costs $8.00 but the cost of the fruit equals (17 – 8) ÷ 3 = $3 per kilogram. A fruit basket with 5 kilograms of fruits will cost 5 x 3 + 8 = $23.
- Each kilogram of mandarin costs 11 ÷ 4 = $2.75. 10 x 2.75 = $27.50 is the cost of 10 kilograms.
- This is a constant problem. Every person takes 2 minutes to eat an orange. 24 people who begin eating at the same time will take the same amount of time, 2 minutes, to eat one orange each.
- There is not enough information to solve this problem but there are two possible answers.
If Nashi pears cost more than plums, then mangoes cost 2.50 + 1.75 = $4.25 per kilogram than plums.
If plums cost more than Nashi pears, then mangoes cost 2.50 - 1.75 = $0.75 per kilogram than plums. - If the amount of both nectarines and peaches is halved, then the difference is also halved.
3.60 ÷ 2 = $1.80.
- The difference in price is constant thought students are not told what that amount is. In February kiwifruit cost 12 ÷ 3 = $4 per kilogram while apples cost 9 ÷ 3 = $3 per kilogram. The price difference is always $1 per kilogram.
Dear parents and whānau,
In mathematics this week, our focus has been on writing and solving equations. Students are applying their understanding that an equation represents a balance, or sameness. The equals sign represents that two amounts on each side of it are the same, though the operations may look different and represent different operations.
Have your child explain their common sense understanding of these two problems, how they would solve the equation, and justify why their strategy works. Using a calculator is fine, provided your student can explain why they chose the operation they did.
| Find the number that goes in the box to make each equation correct. |
| [ ] - 27 = 51 |
| 7 × [ ] = 161 |
| 300 ÷ [ ] = 12 |
Listen to your student’s explanations, and ask questions if the strategies don’t make sense to you. Compliment them when their explanation is clear, and their solution is efficient and correct.
Thank you