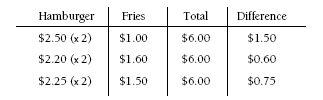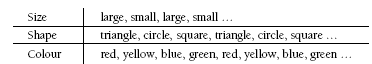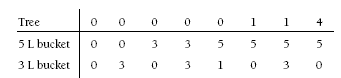These are level 2 number and algebra problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (303 KB)
use additive strategies to solve problems (Problems 1,2 and 4)
predict next member in a sequence (Problem 3)
Problem One
Students are most likely to solve this problem by trial and improvement. Students know that the cost of a hamburger is greater than the cost of fries. A possible method of solving this might be:
Similar types of problems could be posed as extensions, for example:
“A pie costs 50 cents more than a milkshake. Three pies and a milkshake costs $7.50. How much is a milkshake?”
Problem Two
Various solutions are possible, but not all scenarios have all the cars full. One strategy might be to start with 26 counters and experiment by dividing them into threes and fives. A systematic way of doing this is to begin with the minimum number of big cars needed:
Students could investigate how many students would be involved in scenarios where all the cars were full. For example, to take 25 children, five big cars could be used, and to take 21 children, seven small cars could be used.
Problem Three
Students need to be aware of three variables operating in the pattern:
Both questions can be answered by continuing these sequential patterns and relating them to the ordinal numbers. The size, shape, and colour of the fifteenth block can be found by using the repeating element for each variable. For example, the shape variable has a repeating element of three. Fifteen divides by three exactly, so the fifteenth block must be a square. Similarly, the colour variable repeats itself in every fourth object. Because fifteen divides by four with a remainder of three, the fifteenth block is coloured blue, the third colour in the sequence. Odd-numbered blocks are
large, and even-numbered blocks are small, so the fifteenth block must be large.
Students can be encouraged to create their own repeating patterns involving two or more variables.
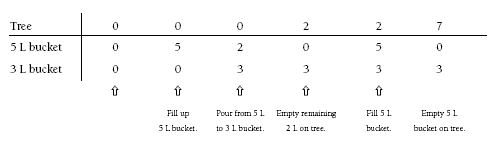
Problem Four
Students may need to record their attempts in an organised way. For example:
Similarly, the problem could be modelled using cut-down 2 litre drink bottles with markings on them.
Check to see whether the students have understood the process by changing the problem to “How could Filo give the tree 4 litres of water?”
A solution to the problem would be:
Fill up the 3 L bucket and pour it into the 5 L bucket.
Fill up the 3 L bucket again and pour it into the 5 L bucket until the 5 L bucket is full.
This will leave 1 L in the 3 L bucket. Water the tree with this.
Fill the 3 L bucket once more and pour it on the tree.
Answers to Problems
1. $2.25
2. 4 big cars and 2 small cars
3. a. small yellow triangle
b. large blue square
4. Fill the 5 L jug and use this to fill the 3 L jug, so there is 2 L in the large jug.
Use the 2 L to water the tree. Then refill the 5 L jug and water the tree with this. The tree will receive 7 L of water.