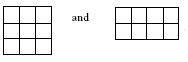These are level 3 number and algebra problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (261 KB)
use addition and multiplication to solve problems (Problem 1)
continue a sequential patterns (Problem 2)
FIO, Levels 3-4, Problem Solving, Following On, page 7
Copymaster of Problem 3 nets
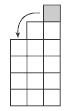
Problem One
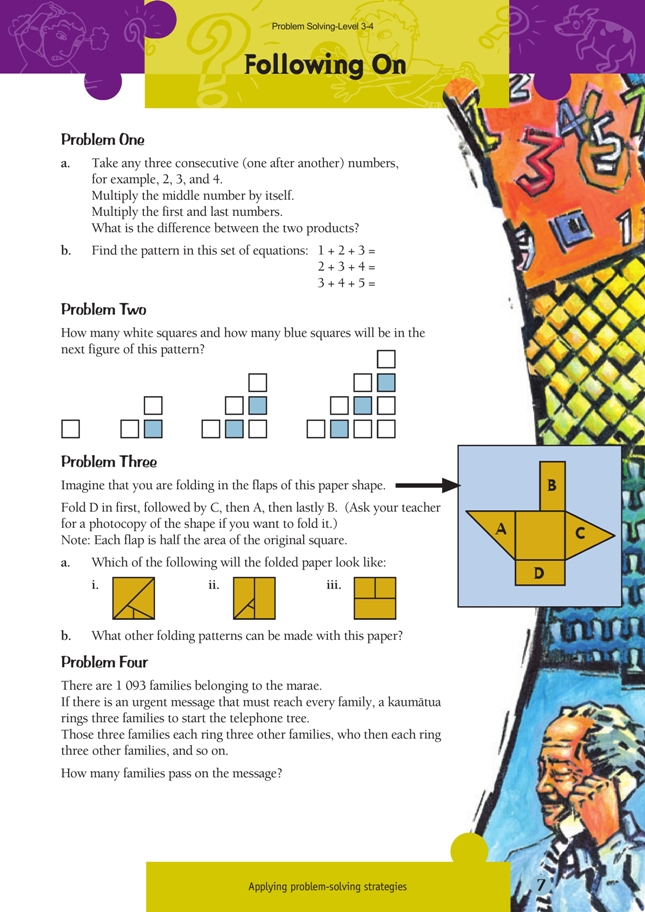
a. One way of setting this out is:
(3 x 3) – (2 x 4) = 9 – 8 = 1.
Using cubes to model it is another useful way for students to get a sense of what’s happening:
“You’ve got
Rearrange one set of blocks to get the other set of blocks. How many more or fewer blocks do you need?”
Extension
You could investigate with the students whether this always works with three consecutive numbers.
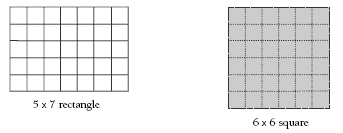
A useful way to explain this to the students is to draw a diagram. For example, for the numbers 5, 6, and 7, investigate the difference between a 5 x 7 rectangle and a 6 x 6 square:
If you lay the shapes over the top of each other, you will see the difference:
Both diagrams have a 6 x 5 rectangle in common. What is the difference between the
leftover areas, that is, the 6 x 1 horizontal strip and the 1 x 5 vertical strip? The difference is 1. The students should find that the same difference will apply using any three consecutive numbers.
b. This pattern works because the first number is one less than the second number and the third number is one more than the middle number. The “one more than” and “one less than” cancel each other out to make three numbers that are the same as the middle number.
Modelling this with cubes is a useful way to explain it to the students. For 4, 5, and 6, put rows of four cubes, five cubes, and six cubes next to each other.
Take a cube from the six-cube pile and add it to the four-cube pile. This makes three equal rows, each with five cubes in them.
So the sum is 3 x 5 = 15. The sum will always be three times the middle number.
The “one less than” and “one more than” cancel each other out because the operation used is addition.
Problem Two
There are several patterns in these figures that students can use to find the number of squares in the next figure. They may notice that the total number of squares in the figures are triangular numbers. They should also see that the number of blue squares increases by one for each consecutive figure and that the number of blue squares is one less than the position of the figure in the pattern (for example, for the fourth figure, there are 4 – 1 = 3 blue squares), or one less than the number of squares along the bottom line, or one less than the longest diagonal line of white squares.
One way to find the number of blue and white squares in the next (fifth) figure is as follows:
The number of blue squares is either one more than in the previous figure (3 + 1) or one less than the number of the figure (5 – 1), both of which are 4.
The total number of squares is the next triangular number (15).
Therefore the number of white squares = total squares – blue squares
= 15 – 4
= 11
Some students may prefer to draw a table to record the number of black, white, and total squares in each figure and then find and continue the pattern for each number of squares.
Extension
Challenge the students to find the number of black and white squares in the hundredth figure. They’ll need to find a quick way to add the numbers from 1 to 100. A method for doing this is explained in the notes for Problem One, page 1.
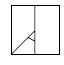
Problem Three
You will find a copymaster of this shape at the back of these notes.
a. This problem can be solved by working backwards. The last piece that was used was piece B, so nothing can be over the top of that piece. And when B comes down, it will form a rectangular shape on the right of the square. The only one with a rectangle down the right side is ii.
b. Rather than the students experimenting by folding the shape parts, encourage them to look for strategies. The basic question is how many different combinations and orders are there of the four letters. The students could solve this in the same way as Problem Three, page 3 (see the notes for this problem), by using a tree diagram and calculating 4 x 3 x 2 x 1. A systematic list, such as that shown in the Answers, is one way of showing the folds.
Problem Four
At each round, the number of families being contacted increases by a factor of 3. The brackets show the total number of families contacted after each round, including the kaumàtua’s family.
Therefore you need six rounds to get in touch with any number of families from 365 to 1 093.
The students will probably recognise that this is another problem that uses exponents. The number of families called in each round are the powers of 3 (that is, 30 = 1, 3 1= 3, 32 = 9, 33 = 27, and so on). So the total number of families called after each round is the sum of the powers of 3. Students may be able to use this as a more efficient way to solve the problem.
Hints for Students
1. Experiment with different groups of three consecutive numbers. What happens every time?
2. You could draw the next figure or you could look for patterns in the number of squares.
3. You could work backwards, draw a diagram, or practise with a photocopy of the shape.
4. Think of this in terms of rounds of calls. How many people will be contacted after the first round? After the second round? How many rounds will be needed? (This is a good problem to try a smaller case first.)
Answers to Problems
1. a. 1
b. The sum is always three times the middle number. (Also, the first and last numbers
add up to twice the middle number.)
2. 11 white, 4 blue
3. a. the picture labelled ii.
b. Including the one shown in the problem, there are 24 ways in which the paper shape can be folded. (The four letters refer to the fold sequence: for example, ABCD means first fold A, second fold B, then C, then D.)
4. 364 families (1 → 3 → 9 → 27 → 81 → 243 → 729.
The last 729 families did not have to pass the message on. 1 + 3 + 9 + 27 + 81 + 243 = 364. 364 + 729 = 1 093.)