This unit examines regular tessellations, that is, tessellations that can be made using only one type of regular polygon, and semi-regular tessellations, where more than one type of regular polygon is involved. Students are required to investigate what properties tessellating shapes must have in order to cover the plane with no gaps or overlaps.
- Create regular and semi-regular tessellations of the plane.
- Demonstrate why a given tessellation will cover the plane.
Tessellations are frequently found in kitchen and bathroom tiles and lino. You can see them in the pattern on carpets and decorative patterns on containers and packaging. They play a significant role in tapa cloth design and creation, and in Islamic art that features designs commonly built around star polygons. Tessellations are a neat and symmetric form of decoration. They also provide a nice application of some of the basic properties of polygons.
To be able to fully understand the concept of tessellations using regular polygons, you need to recognise their symmetry, and be able to calculate the size of their interior angles. This information is accessible to Level 4 students. In this unit, students are led through the steps needed to establish that there are only three regular polygons that tile the plane. This unit follows on from Keeping in Shape from Level 3, where regular tessellations are first discussed.
Moving on from here, the children can consider semi-regular tilings. All that they need to know here is how to sum the interior angles of various regular polygons to 360°. The rest is up to their imagination.
This unit is designed for students to learn and practise outcomes at Level 4 of mathematics in the New Zealand Curriculum. The geometric focus opens up opportunities for visual reasoning that might prove engaging for students who find numeric reasoning challenging. Here are some approaches to enabling participation.
- providing physical manipulatives, regular polygons, or virtual equivalents, so that students can experiment with shapes
- encourage anticipation of results when manipulating polygons, e.g. Will regular hexagons tessellate? How do you know?, and ask students to justify why they believe patterns occur
- directly modelling examples of tessellations, and explaining your reasoning about why the combinations of shapes around each vertex will work
- organising the data about regular polygons in a table, especially the measures of internal angles. Make the table accessible to students so they can make predictions about sets of shapes that will and will not tessellate
- encouraging students to work collaboratively in partnerships, and to share and justify their ideas. Share ideas with the whole class regularly.
The difficulty of tasks can be varied in many ways including:
- allowing access to calculators and digital tools, so the investigations are more about spatial reasoning than calculation
- restricting the set of shapes at first, e.g. triangles, squares, pentagons and hexagons, until generalisations about angles around a vertex emerge. Then open the investigation to more complex regular polygons
- displaying the work of students as models for others, especially students who provide explanations about why particular tessellations work. Motivate students to add a new, undiscovered tessellation to the class display.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Investigate the use of tessellation in cultural designs such as the mosaic art and architecture of the Moors, Greeks, and Persians in Europe and China and Japan in Asia. For example, tessellations are prominent in Islamic art traditions, and in tapa cloth designs from Pacific nations. Students might be fascinated by the work of Dutch artist Escher, who built his work on distorting regular polygons to create ‘life-like’ tessellation patterns. Tessellation might fit well with efforts to beautify the school environment, such as creating a class mural. Mosaic tiles can be created from fired clay, or cobblestones created from concrete.
- Isometric dot paper
- Pattern blocks or mosaic shapes
- Protractors, scissors, paper, rulers, pencils
- Copymaster 1 (table showing angles of regular polygons)
- Copymaster 2 (templates of regular polygons from 3-sided to 12-sided)
- Copymaster 3 (semi-regular tessellations)
- Copymaster 4 (regular polygonal tessellations with different vertex arrangements)
Getting Started
Show the students a large cut out equilateral triangle. Mark the vertices (corners) of the triangle with different colours. Say, "I am going to tear off the corners of this triangle and place them around this point (draw point on board). What do you think will happen?" Students may have encountered this before but let them guess what they think will happen. Tear off the corners and place them about the point to confirm that a half turn (or 180°) is created.
- Ask students whether they think every triangle will produce a 'half turn', no matter what shape it is (isosceles, scalene, obtuse). You may need to display pictures of different types of triangles to support students in this thinking. Is there a way to check this without tearing off the corners? (Measure the interior (inside) angles to see if they total 180° - a half turn.) Tell the students to make a variety of triangles and test this conjecture.
If the sum of the interior angles of any triangle is the same - 180°, is it likely that the sum of the interior angles of any quadrilateral is the same? Ask them to predict what will happen if the corners of any quadrilateral are joined about a point. Have them cut out several quadrilaterals of different shapes to check their predictions. Remind them to mark the corners before tearing them off.
Once it has been found that the sum of the interior angles of any quadrilateral is 360° (they form a full turn about a point), then students can investigate the sum of interior angles of other polygons by measuring with protractors or tearing corners. You may need to model how to find the size of an angle using a protractor. The results can be captured in the table below. Encourage the students to look for a pattern to predict what the next angular sum will be.
Number of Sides
Sum of Angles °
Interior Angle of Regular Polygon
3
180
4
360
5
540
6
720
Note that for each side that is added, the sum of the interior angles increases by 180°. This can be explained by the fact that the addition of a side creates another triangle within the shape, and that each triangle has an angular sum of 180°.
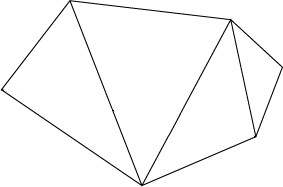
Quadrilateral (2 triangles) Pentagon (3 triangles) Hexagon (4 triangles) - Challenge the students to use their results to draw a regular triangle (equilateral), a regular quadrilateral (square), a regular pentagon, a regular hexagon, and a regular octagon. Regular means that all sides are the same length and all interior angles are equal.
What size are the interior angles of the regular figures we have just been talking about? How can we find out?
For the regular hexagon with six vertices and an angular sum of 720°, we need to divide the sum by the number of angles to find each angle size. So, since 720 ÷ 6 = 120, each interior angle in a regular hexagon is 120°.
- Get the children to complete the table above for polygons with up to 12 sides. (The regular dodecagon (12-sided polygon) has an angular sum of 1800°, so each interior angle will be 150°.)
Exploring
Use a set of pattern blocks to show how equilateral triangles tessellate. Tessellate means that they cover the plane infinitely with no gaps or overlaps. Send the students away in groups with their own set of pattern blocks, or access to an online version (search for Pattern Block Virtual Manipulative), to explore what other tessellations can be discovered using shapes from the set. You may want your students to record the tessellations using isometric dot paper.
After a period of exploration, bring the class back together to share the tessellations. Note that there are three regular tessellations that can be found, that is tessellations involving use of the same regular polygon. These regular tessellations are 3.3.3.3.3.3 (six triangles about each point or vertex), 4.4.4.4 (four squares about each vertex), and 6.6.6 (three hexagons about each vertex).
Focusing on the regular tessellations ask why it is that these patterns work without gaps or overlaps. You may need to remind the students of the angle measures they found in Getting Started. There are two key properties of the shapes involved in regular tessellations:
- side lengths are the same;
- the sum of angles meeting at each vertex is exactly 360° (a full turn). For example, in the case of the tessellation with squares (4.4.4.4), the side lengths are the same and the four angles of 90° add up to 360°. Confirm that the "angles around a point" principle holds for the other tessellations that students have found.
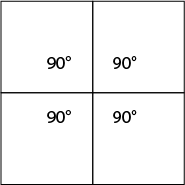
- Remind the students of the table on angle sums (Copymaster 1) that contains the interior angle measurements for regular polygons. Ask: From the table could we have expected the triangles, squares, and hexagons to have tessellated by themselves? How? (Each of these shapes has interior angles that can be divided into 360° evenly.)
- Many other tessellations are possible with combinations of pattern block shapes. Get your students to experiment with combinations of regular polygons. These tessellations are known as semi-regular tessellations. For example, from the table it looks like 2 squares and three triangles might fit together about a point because 90°+ 90°+ 60°+ 60°+ 60° = 360°.
- These might be arranged in different ways, e.g. square-triangle-triangle-square-triangle (4.3.3.4.3) and square-square-triangle-triangle–triangle (4.4.3.3.3). Try to produce all possible combinations using pattern blocks.
- Give the students Copymaster 2 that gives templates for the regular polygons up to the 12-sided shape (dodecagon). By stapling through the centre of each shape onto blank pages underneath students can make multiples of each regular polygon. Ask students to use the table and the cut out shapes to find as many semi-regular tessellations as they can.
- Share the results as a class to see if all the possible semi-regular tessellations have been found. These are 3.3.3.4.4, 3.6.3.6, 3.3.4.3.4, 3.3.3.3.6, 4.8.8, 3.4.6.4, 3.12.12, 4.6.12 (eight possibilities). Students may wish to create a poster presenting their favourite semi-regular tessellations explaining why each combination of shapes can tessellate the plane. Other tessellations are possible using regular polygons if the constraint of each vertex having the same arrangement of shapes is removed. For example, hexagons, squares and triangles can be used in this way.
Note that with some vertices the arrangement is 6.3.4.4 and at others it is 6.4.4.3 if the shapes are read clockwise about each vertex. - Get the students to investigate what other arrangements can be found in this way. Copymaster 4 contains examples of such arrangements. Note that this embodies the principle seen in the square-square-triangle-triangle-triangle arrangements that changing the order of the addends does not affect their sum, in this case 360°.
Reflecting
- Observation of the table might persuade your students that tessellating combinations are not likely for the heptagon (7 sides), decagon (10 sides) and hendecagon (11 sides) since their interior angles measures will not yield combinations to 360°.
- Ask: Is it possible to show that there are only three regular tessellations?
There are two approaches for this depending on the ability of your students. The first way is to notice that no polygon has an interior angle greater than 180°. They are always less than this. And no polygon has an interior angle smaller than 60°(from the table.) That means that you need at least three polygons to come together at a vertex and no more than six polygons since 6 x 60° = 360°:- if it is 3, the interior angles have to be 360°/3 = 120°;
- if it is 4, the interior angles have to be 360°/4 = 90°;
- if it is 5, the interior angles have to be 360°/5 = 72°; and
- if it is 6, the interior angles have to be 360°/6 = 60°.
Only three of these are possible for regular polygons. The only tessellation by regular polygons requires an equilateral triangle, a square or a hexagon.
- How can we find semi-regular tessellations in a systematic way? One way is to start with six triangles around a point. Take away triangles until a different regular polygon will fit in the angle ‘gap’. Remove two triangles leaves a gap of 120° so a regular hexagon will fit. Remove three triangles and there is a gap of 180° that can be filled by two squares. Remove four triangles and two hexagons can fill the gap. Remove five triangles leaves a gap of 300° and two dodecagons, or two squares with a hexagon, can fill the gap. Once all the possibilities with triangles are exhausted, move onto squares around a point and repeat the strategy, ignoring triangles.
- Beginning with 4.4.4.4 and removing two squares leaves a missing angle of 180°. That angle gap might be filled with one triangle and one hexagon but that has already been found above. However, removing 3 squares from 4.4.4.4 leaves a gap of 270° that can be filled with either 2 octagons or 1 dodecagon and 1 hexagon. This gives two new semi-regular tessellations 8.4.8 and 12.6.4.
Dear family and whānau,
This week we have been experimenting with tessellation of the plane with polygons. In particular we have found that regular tessellations can only be made with equilateral triangles, squares and hexagons.
Regular polygons have all sides equal and all angles equal.
- Can you find a shape that has all sides equal but is not a regular polygon?
- How about a shape that has all angles equal but is not a regular polygon? (is this actually possible?)