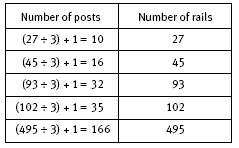Fencing

By this stage, students should be starting to realise that algebra is about the general rule that works rather than about specific numbers. In this activity, students continue to use equations or rules to capture the behaviour of patterns and extend or adapt known rules to cover new, but related, cases.
The diagram in question 1 shows that a fence with 3 sections has 4 posts and 9 rails. The students will need to see that each section has 3 rails and that for any fence, there is always 1 more post than there are sections. Some students may need to draw a fence with 1 section, a fence with 2 sections, and so on to help them visualise these relationships. So for a 37-section fence, there are 37 + 1 = 38 posts and 37 x 3 = 111 rails. And for a fence with n sections, there are n + 1 posts and n x 3 or 3n rails.
In question 2, attention shifts from sections to the link between posts and rails. Tyson’s drawing is designed to help the students to visualise a short cut for counting rails. There are 3 rails for each of the first 3 posts in a 4-post fence. So for a 7-post fence, 6 posts each have 3 rails, giving 18 rails altogether. Some students may need to draw the posts and rails for different fences before they “see” and can use the rule for calculating the number of rails for a fence with any number of posts. So a fence with x posts will have (x – 1) x 3 rails. We usually ignore the times sign and write this as 3(x – 1). Note that if x is the number of posts, then (x – 1) is the number of sections in the fence.
In question 3, you might want to ask the students to first check their fence drawings to see if they can explain how to find the number of posts for a fence with 27 rails. This entails visualising sets of 3 rails attached to all but the last post. So for 27 rails, they visualise 9 posts (from 27 ÷ 3), each attached to sets of 3 rails. There is 1 additional post, so altogether there are 9 + 1 = 10 posts in the fence. So a fence with y rails will have (y ÷ 3) + 1 posts. We usually write this in fraction form as y/3 + 1.
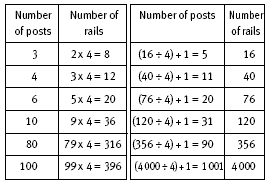
The diagram in question 4 shows a fence with 4 rails in each section between  djacent posts. So a fence with 6 posts can be visualised as having 5 posts each attached to 4 rails. The tables provide opportunities for the students to see how the strategy for a fence with 6 posts can develop into a rule for fences with any number of posts. The algebraic rules for fences with x posts and y rails when there are 4 rails in each section are y = 4(x – 1) when you know the number of posts and x = y/4 + 1 when you know the number of rails. Both of these equations rely on the fact that every post except the last has 4 rails attached.
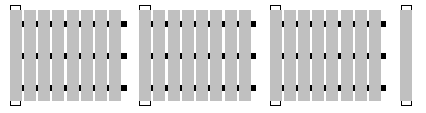
This extended diagram for question 5 shows the palings on a fence with 4 posts.

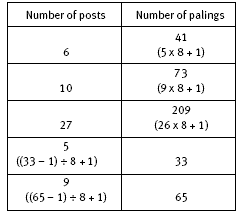
All but the last post has 8 palings attached to the rails, which in turn are attached to the post. The last post has just 1 paling attached to it. So a fence with 4 posts has 3 x 8 + 1 palings. As earlier, some students may need to draw fences with different numbers of posts to help visualise such a short cut. For 6 posts, there are 5 x 8 + 1 palings. So for x posts, there will be (x – 1) x 8 + 1 palings. This is usually written as
8(x – 1) + 1. The students will be using this rule to find the number of palings in question 5b, even though they are not using the algebraic notation to express it. To find the number of posts in this question, given the number of palings, subtract 1 from the number of palings, divide the answer by 4 to get the number of sections, and add 1 for the extra post (the number of posts is always 1 more than the number of  sections).

Answers to Activity

1. a. Tyson is right. A 1-section fence has 2 posts and 3 rails; a 2-section fence has 3 posts and 6 rails; and a 3-section fence has 4 posts and 9 rails. So the number of posts is always 1 more than the number of sections. A 10-section fence has 10 + 1 = 11 posts. Each section has 3 rails, so a 10-section fence has 10 x 3 = 30 rails.
b. 37 + 1 = 38 posts, and 37 x 3 = 111 rails.
2. a. 6 sets of 3 or 6 x 3 rails
b. For a fence with 7 posts, you can think of sets of 3 rails being attached to just 6 of the posts (1 fewer than the total number of posts).
3. a. Tyson is right. The 27 rails are attached to 27 ÷ 3 = 9 posts, but another post is needed to complete the fence. So there are 10 posts altogether.

4. a. A short cut is 5 x 4 rails because 5 of the 6 posts have 4 rails attached.
b.

5. a. 5 x 8 + 1 = 41. A fence with 4 posts has 3 sets of 8 palings and 1 additional paling, which is 3 x 8 + 1 palings. So a 6-post fence will have 5 x 8 + 1 palings.

b.