The focus of this measurement unit is around finding linear patterns. This is explored through Pick’s Rule which applies to finding areas of polygons where all the vertices are lattice points (in this application, the nails on geoboards).
- Find areas of shapes.
- Find simple two-variable linear patterns relating to areas.
This unit concerns a very unusual formula for finding area, Pick’s rule. The mathematics is more challenging than most linear pattern work in that students will need to learn that the establishment of linear patterns in two variables is assisted by first holding one of the variables constant, and finding a linear formula. Changing the value of that variable and again holding it constant produces another similar linear formula. Continuing this process produces a set of formulae from which students can infer a linear formula in two variables.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- grouping students flexibly to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- apply the gradual release of responsibility to scaffold students towards working independently
- allowing the use of calculators to estimate and confirm calculations
- encouraging students to describe expressions and linear patterns in words, and scaffolding them towards the use of symbols
- providing frequent opportunities for students to share their thinking and strategies, ask questions, collaborate, and clarify in a range of whole-class, small-group, peer-peer, and teacher-student settings.
This unit is focussed on investigating Pick's rule, and as such is not set in a real world context. You can increase the relevance of the learning in this unit by providing ample opportunities for students to create their own problems, create their own representations of a task, and participate in productive learning conversations.
Te reo Māori kupu such as tauira (pattern), ture (formula, rule), and horahanga (area) could be introduced in this unit and used throughout other mathematical learning.
Session 1
In this session, students use Geoboards and rubber bands to explore the area of a triangle in a variety of cases, before establishing the rule for finding the area of a triangle. Note that one side of each triangle should be parallel to the vertical or horizontal. Session 2 deals with the case where none of the sides are vertical or horizontal.
- Introduce students to the Geoboards, and give them time to explore them. Demonstrate how shapes can be made by looping the rubber bands over the nails. Gradually structure students' exploration of Geoboards towards making triangles:
What shapes can you make?
How many different sized squares can you make?
How many different triangles can you make? - Explain to students that this session will involve making triangles and calculating their areas. Confirm with students that area is the measure of the size of a two-dimensional surface that is measured in square units. Ask each student to make a triangle on their Geoboard. At least one side of the triangle should be either horizontal or vertical. The picture shows the three types of triangle they might make.
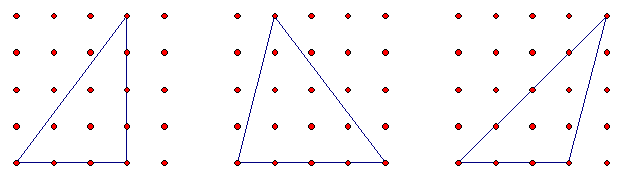
- Ask students to add rubber bands around their triangle to make a shape that is easier to find the area of; The next pictures illustrates typical solution methods found by adding rubber bands.
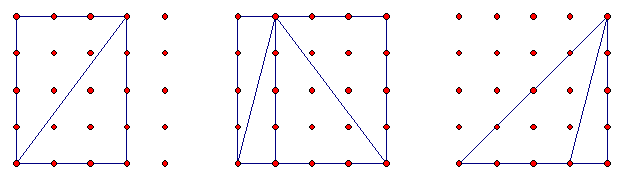
Looking at the first shape, the area of the triangle is equal to half the surrounding rectangle. In the second shape, the area of the triangle is half of each of two surrounding rectangles. These two rectangles make up the large rectangle. In both cases the area of the original triangle is half the surrounding rectangle or 1/2 bh (1/2 base x height). In the third example, the triangle is the same as the large right angled triangle minus the small right angled triangle. The fact that this is still 1/2 bh where the height is outside the obtuse angled triangle deserves careful discussion.
- Allow students time to make more triangles and find their areas. Roam and provide support to students, ensuring they calculate the area of each triangle correctly. As an extension, students could investigate the area of other regular polygons using the Geoboards.
Session 2
In this session students apply their knowledge of rectangles and triangles by using Geoboards and rubber bands to find the areas of polygons.
- Give students a few examples of relatively simple polygons to find the areas of. For example see picture below.
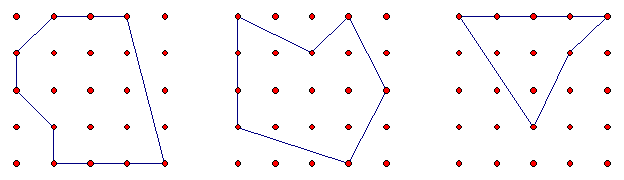
- Work through a couple of examples as a class to ensure that all students can see that the areas can most easily be found by breaking the shapes up into rectangles and triangles, or by enclosing the shape in a rectangle and finding the areas of any parts that are not included.
- Challenge students to find the areas of the polygons on Copymaster 1.
- Allow students to pair up and create polygons to challenge each other with. As an extension, you could ask students to create word problems that apply this mathematical content within reflect a current, relevant context.
Session 3
This session introduces the beginnings of Pick’s rule. Pick’s rule for the area of a polygon drawn on a grid is A=1/2 b+i-1 where A is the area, b = number of dots on the boundary of the polygon, and i is the number of dots inside the polygon. Students are scaffolded to slowly build towards Pick’s rule.
- Explain to students that you wanted to teach them a rule that you can use to work out the areas of shapes on a Geoboard but that you can’t quite remember what the rule was. All you can remember is that you had to count the posts that were used.
- Ask for suggestions from the class as to how you could work out the rule. Hopefully someone will suggest a systematic approach. Suggest that they might want to start with a simple shape – the triangle. Give students some time to gather information, drawing (or making on a Geoboard) several triangles and calculating their areas.
- Discuss students’ findings as a group:
Did you find any patterns?
Were you systematic in what triangles you drew?
What did you notice about the triangles that had the same areas?
- Suggest that the class develop a system for choosing what triangles to draw. Suggest that they group their triangles by how many posts they have inside them (not including any that touch the sides) Start with triangles with 2 inside posts. Ask students to work in groups to draw as many different triangles with two inside posts as possible.
- Bring the whole class back together to discuss what they have found out
Do triangles with the same number of posts inside have the same area? (Not necessarily).
What do you notice about the triangles with the same number of inside posts that do have the same area? (They have the same number of posts on their boundary).
Ask individual groups to try to come up with a rule for their set of triangles.
The rules they should come up with are variants of Pick’s rule (A=1/2 b+i-1) though they may need to express parts in words rather than algebraically:
For 2 inside posts: A=1/2 b+1
Some students are likely to give a rule such as “For 2 inside posts the area is two and a half if there are only three posts on the boundary, plus an extra half for each extra post on the boundary.” Encourage them to try to write it using symbols.
If there is time left in the session groups could be challenged to try to find a similar rule for triangles with 0, 1, 3, or 4 inside posts Alternatively, this could be the start of the next session.The rules should be:
For 0 inside posts:A=1/2 b-1
For 1 inside post:A=1/2 b
For 3 inside posts:A=1/2 b+2
For 4 inside posts:A=1/2 b+3
Session 4
In this session students extend on the work they did with triangles in the previous session, to generalise the rule and to see that it applies to all shapes, not just triangles.
- Begin the session by going over the rules found in the previous session.
- Distribute Copymaster 2 and have students attempt the problems. Bring the class back together after each question to ensure that they are on the right track. Students should quickly see that the rules they found for triangles apply here for any polygon. They should still be thorough in testing for different numbers of inside posts. Challenge them to find a polygon which doesn’t follow the rules. Some discussion and support may be required to answer Question 4. The rule for any number of inside posts and any number of boundary posts is A=1/2 b+i-1 (Pick’s rule).
- Ask students draw their own irregular polygons on dotted paper and compute the area as in session 2 and also by Pick’s rule A=1/2 b+i-1. Have students compare their answers in pairs. If they are different they should endeavour to self-correct by detecting whether the error is in finding the area or in their calculation.
Session 5
This session is an extension for more able students. A challenge is to generalise Pick’s rule when some regions are subtracted. Copymaster 3 is a blank grid of dots that can be used by students during this investigation.
- Get the students to draw a set of simple shapes on Copymaster 3 with one region inside like these:
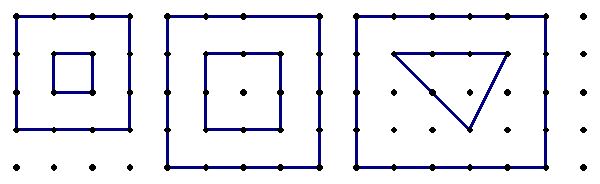
- Ask students to calculate the areas of each shape, excluding the inner part.
- Compare this against Pick’s rule A=1/2 b+i-1 where the counts for b includes the dots on the inside boundary and the inside dots of the inner shape are ignored. It is then evident that Pick’s rule consistently is 1 less than the true area. Thus the conjecture is that A=1/2 b+i when there is one inner region.
- Continue to investigate with two inner regions:
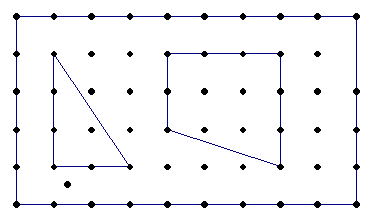
- Here Pick’s rule consistently is 2 less than the correct answers implying that the rule for two inner regions is A=(1/2 b+i-1)+2
- Students should now proceed to find a formula when there are n inside regions. Pick’s rule generalised becomes A=1/2 b+i+n-1
Dear families and whānau,
Recently we have been investigating Pick's rule. This is a rule related to area. Ask your child to share with you what they know about Pick's rule, and have them draw a diagram demonstrating Pick's rule.