This problem solving activity has an algebra focus.
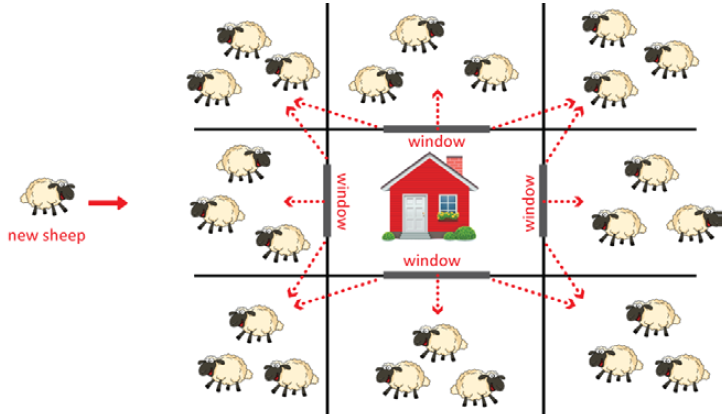
A farmer can see nine sheep if he looks out of any of his four windows.
His wife buys him a new sheep.
Which paddocks can he put the new sheep in so that he can still see nine sheep from each of the four windows?
In how many ways can the farmer put his 25 sheep so that he can see 9 sheep through each window?
(Every paddock is to have at least one sheep.)
- Devise and use problem solving strategies to explore situations mathematically.
This problem helps to develop students' problem solving skills, logical thinking and their ability to work sequentially. It also helps develop rules for mathematical problems. These rules may not be obvious at first.
This problem is further developed in Level 4 Algebra problem The Farmer’s Sheep II.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Counters or plastic animals (or digital representation)
- Large grid (or digital representation)
The Problem
A farmer can see nine sheep if he looks out of any of his four windows. His wife buys him a new sheep. Which paddocks can he put the new sheep in so that he can still see nine sheep from each of the four windows?
In how many ways can the farmer put his 25 sheep so that he can see 9 sheep through each window? (Every paddock is to have at least one sheep.)
Teaching Sequence
- Tell the students the story of a farmer who only likes to be able to see nine sheep from his window. His wife has bought him another sheep what is he going to do? Where can he put it?
- Put a large version of the grid up in the classroom and point out the features e.g. where the windows are.
- Explain the rules:
The new sheep must go in a paddock, it cannot be destroyed, hidden, eaten, etc.
The farmer must be able to see a total of nine sheep from the three paddocks he can see from each window. - Encourage the students to work in pairs and record the problem solving sequences they go through.
- Share solutions. Is there a rule?
Solution
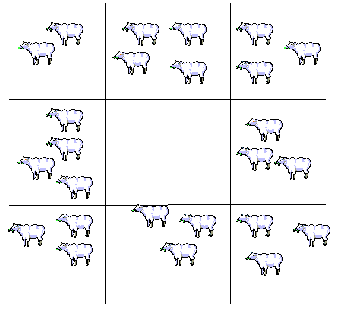
Perhaps the simplest way to do this problem is to notice that you can move one sheep from the top right hand paddock to the left centre one. This keeps 9 sheep in view from each window except the one at the top. If you put one sheep in the centre top paddock this balances up the problem.
There are however many ways of doing this problem but they all need a lot more moving of sheep. Students might suggest other solutions.
The guess and check method will work, but may take some time. When students have a few more solutions, they might begin to see a pattern. Surprisingly, in every case, the numbers of sheep in the four corner paddocks always adds up to 11. Why is this?
The following argument may be a bit complex but some of the more advanced students will be able to see what is happening. Suppose that we added together all of the sheep that can be seen from the four windows. The sum would be 36 (= 4 x 9). But if we add up all those sheep we are adding up the corner paddocks twice and the other paddocks once. So we are adding together every paddock once and the corner paddocks once more. ‘But every paddock once’ gives us all the sheep there are. This is 25. So 25 + the sheep in the corner paddocks = 36. This means that the corner paddocks have to have 11 sheep in them.
A systematic approach gives all the 16 answers below.