The Factoring Factory

Activities One and Two

These activities require students to consider how one factor in a multiplication or the divisor in a division can be partitioned by factorising. At the advanced additive stage, students learn to partition one factor in a multiplication additively. For example, the student might solve 7 x 15 as 7 x 10 + 7 x 5. The 15 has been partitioned into 10 + 5. This is an example of the distributive property at work.
Advanced multiplicative students should recognise that they can also partition numbers by factors.
For example, they could rewrite 8 x 17 as 17 x 8 and solve it using 2 x 2 x 2, which is a factorisation of 8. Using a doubling strategy, they could solve this easily as 17 x 2 x 2 x 2 (that is, 34, 68, 136). Similarly, they could solve 216 ÷ 12 as 216 ÷ 2 ÷ 2 ÷ 3 (that is, 108, 54, 18), where 2 x 2 x 3 is a factorisation of 12.
Knowing how to factorise is a key to understanding equivalent fractions and more complex work such as dividing fractions and decimals. For example, finding of (that is, x = ) involves recognising that 3 x 5 is a factorisation of 15.
For a lesson on how to teach multiplicative partitioning by factors, refer to pages 38 to 40, Book 6: Teaching Multiplication and Division in the Numeracy Project series.
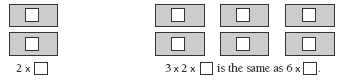
Students who require support with this concept will find strip diagrams useful for imaging. For example, to find the effect of multiplying a number by 2 then 3, you could draw:

A similar diagram could be used to show the effect of dividing a number by 2 and then dividing the result by 3:

Question 4 in Activity Two directs the students’ attention towards prime number factors. The fundamental theorem of arithmetic says that each whole number has a single, unique factorisation made of prime numbers. For example, you can write 30 as the product of prime numbers in only one way, 2 x 3 x 5, and for 14, the prime factorisation is 2 x 7.
In the context of Shaun’s replicating machine, only the prime number settings are necessary. The x 4 and x 6 settings are not needed because the same effect can be produced using prime number factors: x 2 followed by x 2 results in x 4 (just as ÷ 2 followed by ÷ 2 results in ÷ 4), and x 2 followed by x 3 results in x 6 (just as ÷ 2 followed by ÷ 3 results in ÷ 6). Also, x 3 followed by x 3 results in x 9, and ÷ 3 followed by ÷ 3 results in ÷ 9. If Shaun added 7, 11, and 13 to the dials, he could
then create a large number of replications using prime number factors. For example, to produce 110 times anything, he could set the machine at x 2, then x 5, then x 11.

Extension

 The students could investigate problems in which prime number factorisation allows all of the possible factors of a number to be found. For example, The Juice Company wants to design a 330 millilitre carton that fits nicely into people’s hands. They want the container to have edges that measure to an exact number of centimetres. What cuboid-shaped cartons could they make? Which one would fit a hand best?
The prime number factorisation of 330 is 2 x 3 x 5 x 11. Regrouping these factors gives 6 x 5 x 11, 2 x 3 x 55, 2 x 15 x 11, 10 x 3 x 11, 22 x 3 x 5, and 33 x 2 x 5. These factors give the possible dimensions of the carton in centimetres. (1 could also be considered as a factor, but that would make a very thin carton.)
The students could also investigate the significance of prime number factors in finding the simplest form of equivalent fractions. For example, consider the problem “What is the simplest fraction equivalent to 60/84?” One approach is to divide both the numerator (top number) and denominator (bottom number) by the same or progressively larger prime numbers. So 60/84= 30/42 (dividing by 2),
30/42 = 15/21 (dividing by 2), and 15/21 = 5/7 (dividing by 3). When this process gives a numerator or a denominator that is a prime number (both are in this case), the fraction can’t be simplified further.

Answers to Activities

Activity One
1. Shaun had 15 times more coins. (x 3, then x 5 gives x 15.)
2. a. 6 times
b. 12 times
c. 20 times
d. 27 times
e. 60 times
f. 16 times
Activity Two
1. 1/6. (24 ÷ 2 = 12, 12 ÷ 3 = 4; = )
2. a. 1/10. (÷ 2, then ÷ 5 gives ÷ 10)
b. . 1/20 (÷ 4, then ÷ 5 gives ÷ 20)
c. . 1/18 (÷ 6, then ÷ 3 gives ÷ 18)
d. . 1/10 (÷ 5, then ÷ 2 gives ÷ 10)
e. . 1/8 (÷ 2, then ÷ 2, then ÷ 2 gives ÷ 8)
f. . 1/45 (÷ 3, then ÷ 3, then ÷ 5 gives ÷ 45)
3. a. i. x 3, then x 3, then x 3. (4 x 3 x 3 x 3 = 108, and 27 x 4 = 108.)
ii. ÷ 4 ÷ 4 or ÷ 2 ÷ 2 ÷ 2 ÷ 2
b. For a i, there is only 1 combination that would work, but for a ii, there are 2
possibilities because ÷ 2 ÷ 2 has the same effect as ÷ 4.
4. No, only prime numbers are needed on the dials. The x 4 and ÷ 4 dials are not needed because x 2 x 2 and ÷ 2 ÷ 2 have the same effect. The x 6 and ÷ 6 dials are not needed because x 3 x 2 and ÷ 3 ÷ 2 have the same effect.