These are level 3 number and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (310 KB)
use additive and multiplicative strategies to sovle problems using measurement as a context (Problems 1 and 4)
interpret three dimensional drawings (Problem 2)
use multiplication facts to solve problems (Problem 3)
Problem One
Students will need to know that 1 tonne = 1 000 kilograms. So a 3 tonne log has a mass equivalent to 3 000 kilograms. Since one elephant can pull 550 kilograms, six elephants can pull 6 x 550 = 3 300 kilograms.
Students could also divide the total mass of the log by the mass each elephant can pull. 3 000 ÷ 550 = 5.45, so six elephants are needed.
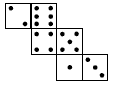
Problem Two
The net shown is not the T shape most commonly used to form a cube. Students may need to build a cube from the net so that they realise how it fits together. Once they know this, they can visualise what the opposite faces will be.
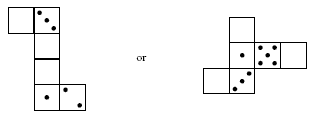
The pairs of opposite faces are shown as A, B, and C. Each pair must have a total of seven dots, so the complete net must be:
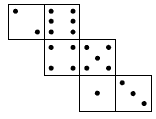
Students may enjoy creating their own dice net puzzles, such as:
Some students may need to make a blank net and fold it to establish which faces are opposite.
Problem Three
This problem involves the concept of common multiples. Room 8 can form an exact number of teams of five for netball, so the possible numbers of students are 5, 10, 15, 20, 25, 30, 35, … They can also form an exact number of teams for mini hockey, so the possible numbers of students are 6, 12, 18, 24, 30, 36, …
The common multiples of 5 and 6 give the number of possible students in Room 8. That is, 30, 60, 90, ....Classes usually comprise about 30 students, so this is the most likely answer.
Providing similar types of common multiple problems will help students to generalise the mathematics involved. For example, “Terry has a stamp collection. He can arrange three stamps on a page of his album with none left over. He can also arrange four on a page with none left over or five on a page with none left over. He has fewer than 100 stamps. How many has he got?” (60).
Problem Four
As with Problem Three, this involves the concept of common multiples. The landing marks of each rabbit are:
Red rabbit 30, 60, 90, 120, 150, 180, …
Purple rabbit 20, 40, 60, 80, 100, 120, …
Pink rabbit 25, 50, 75, 100, 125, 150, …
Although students could continue the multiple patterns to see whether the rabbit lands on the 600 metre mark, dividing by the jump distance is more efficient: 600 ÷ 30 = 20 is the number of jumps for the red rabbit, 600 ÷ 20 = 30 is the number of jumps for the purple rabbit, and 600 ÷ 25 = 24 is the number of jumps for the pink rabbit. In each case, there is no remainder, so the rabbits all land on the 600 mark.
As an extension, give the students other rabbits to consider. For example:
“The green rabbit jumps 40 centimetres each time.” (600 ÷ 40 = 15 jumps)
“The brown rabbit jumps 75 centimetres each time.” (600 ÷ 75 = 8 jumps)
“The blue rabbit jumps 45 centimetres each time.” (600 ÷ 45 = 13.33 jumps) The blue rabbit will not land exactly on the 600 centimetre mark.
Answers to Problems
1. 6
2.
3. Although the answer could be any multiple of 5 and 6, for example, 30, 60, or 90, the most likely answer is 30.
4. Yes. The red rabbit will reach 600 in 600 ÷ 30 = 20 jumps. The purple rabbit will reach 600 in 600 ÷ 20 = 30 jumps. The pink rabbit will reach 600 in 600 ÷ 25 = 24 jumps. 30, 20, and 25 are all factors of 600.