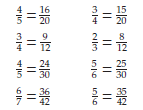Find equivalent fractions and order fractions.
Number Framework Stage 7
Equivalant fractions (Material Master 8-9).
After understanding what a fraction is, equivalent fractions is the next most important concept in fractions. It is needed in all the operations on fractions. In this activity, the fraction shapes are rectangles rather than circles as rectangles are much easier to draw.
Using Materials
Teaching the comparison of fractions requires considerable care.
Problem: “Identical twins Ronald and Donald get identical cakes for their birthdays. Ronald cuts his cake into 4 and eats 3/4 of it. Donald cuts his cake into 5 and eats 4/5 of it. Who has eaten more cake?”
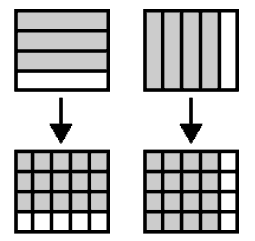
Get the students to draw the cakes as two 8 centimetre by 10 centimetre rectangles using Material Master 8–8. Add horizontal lines to Ronald’s cake and vertical lines to Donald’s cake.
Discuss why you don’t add vertical lines to Ronald’s cake and horizontal lines to Donald’s cake.
(Answer: It is possible, but then the lines do not follow the grid lines.)
Discuss why adding vertical and horizontal lines respectively enables you to compare the shaded areas. (Answer: Each cake now has 20 parts.)
Discuss why for Ronald 3/4 = 15/20 and why for Donald 4/5 = 16/20 .Discuss how this shows 3/4 < 4/5. (Answer:15/20 < 16/20 from the diagrams.)
Problem: “Draw a pair of 8 centimetre by 6 centimetre rectangles on the supplied grid. Add to one rectangle and to the other. Create 12 squares on each and decide whether 3/4 > 2/3 or 2/3 > 3/4.”
(Answer: 3/4 >2/3 because 9/12 > 8/12.)
Examples: Decide which fraction is the larger by drawing rectangles. Carefully plan the size of the rectangles before starting drawing: 4/5 or 5/6 1/3 or 3/7 5/6 or 6/7...
Using Imaging
Problem: “From the examples above, Donna summarises the data and looks for patterns.What patterns can you see?”
Problem: “Donna wonders how to solve 3/7 = ?/28.
Imagine what a rectangle with horizontal lines showing 3/7 would look like. What vertical lines would be needed to cut the whole into 28 equal pieces? Answer the problem 3/7 = ?/28” Fold back to drawing a picture if needed.
Examples: Imagine pictures and complete these: 3/4 = ?/16, 2/3 = ?/15, 5/6 = ?/18, 3/10 = ?/20, 7/9 = ?/27.
Using Number Properties
Examples: Worksheet (Material Master 8–9).
Understanding Number Properties:
Make up a fraction that has a denominator greater than 99 and that equals 4/5.